Предмет динамического программирования

Динамическое программирование

Динамическое программирование (иначе, «динамическое планирование») представляет собой особый математический метод оптимизации решений, специально приспособленный к многошаговым (или многоэтапным) операциям.

Представим себе, что исследуемая операция Q представляет собой процесс, развивающийся во времени и распадающийся на ряд «шагов» или «этапов». Некоторые операции расчленяются на шаги естественно: например, при планировании хозяйственной деятельности группы предприятий естественным шагом является хозяйственный год. В других операциях разделение на шаги приходится вводить искусственно.

Процесс, о котором идет речь, является управляемым, т.е. на каждом шаге принимается какое-то решение, от которого зависит успех данного шага и операции в целом. Управление операцией складывается из ряда элементарных, «шаговых» управлений.

Рассмотрим пример естественно-многошаговой операции Q. Пусть планируется деятельность группы (системы) промышленных предприятий П₁ П₂, П_к на некоторый период времени T состоящий из m хозяйственных лет (рис. 1).

В начале периода на развитие системы предприятий выделяются какие-то основные средства K₀, которые должны быть как-то распределены между предприятиями. В процессе функционирования системы выделенные средства частично расходуются (амортизируются). Кроме того, каждое предприятие за год приносит некоторый доход, зависящий от вложенных средств. В начале каждого хозяйственного года имеющиеся средства могут перераспределяться между предприятиями: каждому из них выделяется какая-то доля средств.

Ставится вопрос: как нужно в начале каждого года распределять имеющиеся средства между предприятиями, чтобы суммарный доход от всей системы предприятий за весь период Т = m был максимальным?

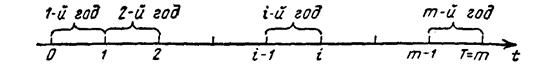
Перед нами — типичная задача динамического про г р а м м и р о в а н и я.

Рассматривается управляемый процесс — функционирование системы предприятий. Управление процессом состоит в распределении (и перераспределении) средств. Шагом управления является выделение каких-то средств каждому из предприятий в начале хозяйственного года,

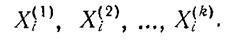Пусть в начале 1-го года предприятиям П₁ П₂, П_k выделяются соответственно средства:

Совокупность этих значений представляет собой не что иное, как управление на i -м шаге:

U_i=(X_i⁽¹⁾, X_i⁽²⁾, …,X_i⁽^k⁾).

Управление может быть хорошим или плохим, эффективным или неэффективным. Эффективность управления U оценивается тем же показателем W, что и эффективность операции в целом. В нашем примере показатель эффективности (целевая функция) представляет собой суммарный доход от всей системы предприятий за m лет. Он зависит от управления операцией U, т. е. от всей совокупности шаговых управлений: Управление U операцией в целом представляет собой совокупность всех шаговых управлений:

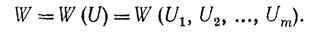
Возникает вопрос: как выбрать шаговые управления U₁, U₂, …, Um для того, чтобы величина W обратилась в максимум?

Поставленная задача называется задачей оптимизации управления, а управление, при котором показатель W достигает максимума, — оптимальным управлением. Будем обозначать оптимальное управление (в отличие от управления вообще U) буквой u. Оптимальное управление многошаговым процессом состоит из совокупности оптимальных шаговых управлений:

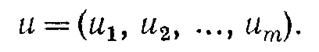
Таким образом, перед нами стоит задача: определить оптимальное управление на каждом шаге u_i (i=1, 2, …, m) и, значит, оптимальное управление всей операцией u.

Заметим, что в нашем примере (управление финансированием системы предприятий) показатель эффективности W представляет собой сумму доходов за все отдельные годы (шаги):

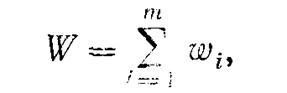
где w_i — доход от всей системы предприятий за i-й год.

Поставим задачу динамического программирования в общем виде. Пусть имеется операция Q с показателем эффективности (1), распадающаяся (естественно или искусственно) на m шагов. На каждом шаге применяется какое-то управление U_i. Требуется найти оптимальное управление

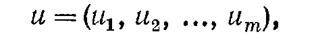
при котором показатель эффективности

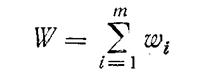
обращается в максимум.

Поставленную задачу можно решать по-разному: или искать сразу оптимальное управление и, или же строить его постепенно, шаг за шагом, на каждом этапе расчета оптимизируя только один шаг. Обычно второй способ оптимизации оказывается проще, чем первый, особенно при большом числе шагов.

Такая идея постепенной, пошаговой оптимизации процесса и составляет суть метода динамического программирования.

При использовании метода динамического программирования следует учитывать то, что шаговое управление должно выбираться с учетом всех его последствий в будущем. Планирование должно быть дальновидным, с учетом перспективы, иначе возможны серьезные ошибки.

Например, пусть планируется работа группы промышленных предприятий, одни из которых заняты выпуском предметов потребления, другие же производят для этого машины. Задачей является получение за m лет максимального объема выпуска предметов потребления. Пусть планируются капиталовложения на первый год. Исходя из узких интересов данного шага (года), мы должны были бы все средства вложить в производство предметов потребления, пустить имеющиеся машины на полную мощность и добиться к концу года максимального объема продукции. Но правильным ли будет такое решение с точки зрения операции в целом? Очевидно, нет. Имея в виду будущее, необходимо выделить какую-то долю средств и на производство машин. При этом объем продукции за первый год, естественно, снизится, зато будут созданы условия, позволяющие увеличивать ее производство в последующие годы.

Таким образом, планируя многошаговую операцию, необходимо выбирать управление на каждом шаге с учетом его будущих последствий на еще предстоящих шагах.

Однако из этого правила есть исключение. Среди всех шагов существует один, который может планироваться без «оглядки на будущее». Очевидно, это последний — после него других шагов нет. Этот шаг, единственный из всех, можно планировать так, чтобы он как таковой принес наибольшую выгоду. Спланировав оптимально этот последний шаг, можно к нему пристраивать предпоследний, к предпоследнему — пред-предпоследний и т. д.

Поэтому процесс динамического программирования разворачивается от конца к началу: раньше всех планируется последний, m-й шаг. А как его спланировать, если мы не знаем, чем кончился предпоследний? Очевидно, нужно сделать разные предположения о том, чем кончился предпоследний (m-1)-й ш а г, и для каждого из них найти такое управление, при котором выигрыш (доход) на последнем шаге был бы максимален. Решив эту задачу, мы найдем условное оптимальное управление на m-м шаге, т. е. то управление, которое надо применить, если (m-1)-й шаг закончился определенным образом.

Предположим, что эта процедура выполнена, и для каждого исхода (m-1)-го шага мы знаем условное оптимальное управление на m-м шаге и соответствующий ему условный оптимальный выигрыш. Теперь мы можем оптимизировать управление на предпоследнем, (m-1)-м шаге. Сделаем все возможные предположения о том, чем кончился пред-предпоследний, (m-2)-й шаг, и для каждого из этих предположений найдем такое управление на (m-1)-м шаге, чтобы выигрыш за последние два шага (из которых последний уже оптимизирован) был максимален. Далее оптимизируется управление на (m-2)-м шаге, и т. д.

Одним словом, на каждом шаге ищется такое управление, которое обеспечивает оптимальное продолжение процесса относительно достигнутого в данный момент состояния. Этот принцип выбора управления называется принципом оптимальности. Само управление, обеспечивающее оптимальное продолжение процесса относительно заданного состояния, называется условным оптимальным управлением на данном шаге.

Теперь предположим, что условное оптимальное управление на каждом шаге нам известно: мы знаем, что делать дальше, в каком бы состоянии ни был процесс к началу каждого шага. Тогда мы можем найти уже не «условное», а просто оптимальное управление на каждом шаге.

Действительно, пусть нам известно начальное состояние процесса, обозначим его S₀. Теперь мы уже знаем, что делать на первом шаге: надо применить условное оптимальное управление, выработанное нами для первого шага, относящееся к состоянию S₀. В результате этого управления после первого шага система перейдет в другое состояние, но для этого состояния мы снова знаем условное оптимальное управление на втором шаге u₂, и т. д. Таким образом мы найдем оптимальное управление процессом

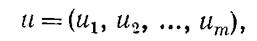
приводящее к максимально возможному выигрышу W_max,

Таким образом, в процессе оптимизации управления методом динамического программирования многошаговой процесс «проходится» дважды:

первый раз — от конца к началу, в результате чего находятся условные оптимальные управления на каждом шаге и оптимальный выигрыш (тоже условный) на всех шагах, начиная с данного и до конца процесса;

второй раз — от начала к концу, в результате чего находятся (уже не условные) оптимальные шаговые управления на всех шагах операции.

Задачи нахождения кратчайшего пути на сети дорог (задача о рациональном маршруте доставки)

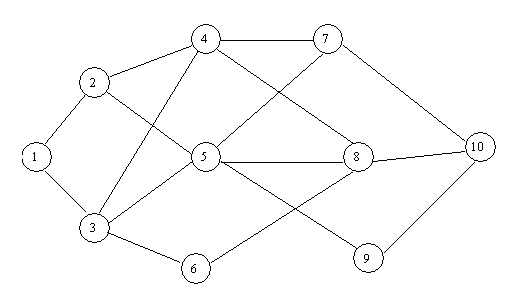
На данной сети дорог указаны стоимости доставки единицы груза из пункта в пункт. Найти наиболее экономный маршрут перевозки груза из пункта 1 в пункт 10.

Решение. Минимизировать затраты по доставке целесообразно применительно к единице груза, ибо понятно, что если затраты минимальны при перевозке единицы груза, то они будут минимальными и при перевозке любого количества груза.

Концепция динамического программирования предполагает, что процессу принятия решения в оптимизационной задаче может быть придан шаговый характер. С этой целью разобьем все пункты сети на группы.

К группе I отнесем пункт 1, к группе II — пункты, в которые можно попасть непосредственно из пункта 1 (таковыми будут 2 и 3), к группе III отнесем пункты, в которые можно попасть непосредственно из любого пункта группы II (таковыми будут 4, 5 и 6), и т. д. В результате движение транспорта с грузом из пункта 1в пункт 10 можно рассматривать как четырехшаговый процесс: на первом шаге транспорт перемещается из пункта 1 в какой-то пункт группы II, на втором шаге — из пункта группы II в пункт группы III и т. д

I	II	III	IV	V

1-й шаг:

	Конечный пункт	Общие минимальные затраты f₁(S)	Конечный пункт на оптимальном маршруте j₁(S)
Начальный пункт S

2-й шаг:

	Конечный пункт	Общие минимальные затраты f₂(S)	Конечный пункт на оптимальном маршруте j₂(S)
Начальный пункт S
	5+3	7+2	-
	6+3	10+2	8+4
	-	3+2	-

3-й шаг:

	Конечный пункт	Общие минимальные затраты f₃(S)	Конечный пункт на оптимальном маршруте j₃(S)
Начальный пункт S
	1+8	3+9	-
	4+8	3+9	2+5

4-й шаг

	Конечный пункт	Общие минимальные затраты f₄(S)	Конечный пункт на оптимальном маршруте j₄(S)
Начальный пункт S
	2+9	3+7