Лекция № 5 Механическая модель вязкой жидкости (тело Ньютона)

Таблица 5 - Классификация пищевых продуктов хлебопекарного, макаронного и кондитерского производства по текстурным признакам и реологическим свойствам.

Реальные тела отличаются от идеальных тем, что в них одновременно присутствуют и упругие и пластические и вязкие свойства. Выражать реологические свойства реальных тел можно механическими моделями. При составлении механических моделей исходят из положения, что де­формация сложного тела является результатом наложения деформаций элемен­тарных механических моделей идеализированных тел, отражающих основные реологические свойства. К основным реологическим свойствам, которые на­блюдаются у реальных тел, относятся: вязкость, упругость и пластичность.

Механические модели, отражающие элементарные реологические свойства.

В реологии различные материалы представляются механическими моде­лями, составленными из простых идеализированных тел. Механические модели позволяют представить, как ведет себя тот, или иной, материал под нагрузкой. По этим механическим моделям составляют математические уравнения зависи­мостей различных параметров: касательных τ и нормальных σ напряжений, угловых γ и линейных ε деформаций, скоростей изменения этих деформаций и т.д.. Зависимости параметров между собой часто изображают на графиках.

В теории реологии используются следующие основные модели идеальных тел: идеально-упругое (тело Гука), идеально-пластич­ное (тело Сен-Венана) и идеально-вязкое (тело Ньютона).

Ни один из пищевых материалов по своим реологическим характеристикам не может соответствовать одному из идеальных тел.

Свойства жидкостей.

Жидкости – вещества, у которых при постоянном напряжении сдвига наблюдается течение, то есть деформация с постоянной или переменной скоростью. Свойства жидкостей проявляются и у пластичных тел после превышения предела текучести. Например, при простом сдвиге ньютоновской жидкости с напряжением сдвига θ возникает деформация с определенной скоростью γ.

Идеально-вязким считается тело, течение которого подчиняется постулату Ньютона и закону Пуазейля, характеризуется тем, что возникающие в ней напряжения пропорциональны скорости деформации. Идеально-вязкое тело чаще называют ньютоновской жидкостью. Вязкость такой жидкости называется нормальной, бесструктурной или ньютоновской, так как она не зависит от скорости сдвига.

Вязкость – способность тела оказывать сопротивление относительному смещению его слоев, мера интенсивности сил внутреннего трения.

Реологическое уравнение состояния ньтоновской жидкости:

θ =ηγ.

η – ньютоновская вязкость, Па∙с.

θ – напряжение сдвига, Па (τ)

γ – скорость деформация, с^-1

Для характеристики жидкостей используют кривые течения – реограммы, которые представляют собой зависимость напряжения сдвига от скорости сдвиговой деформации в условиях простого сдвига. Реограмма ньютоновских жидкостей (водные растворы, вино, жидкое масло при повышенной температуре, молоко, пахта, молочная сыворотка, сливки с масс. долей жира менее 20%) представляет собой прямую линию, которая проходит через начало координат. Для неньютоновских жидкостей вязкость является функцией от скорости сдвига и поэтому называется кажущейся или эффективной вязкостью (η_эф). Неньютоновские жидкости (кисломолочные продукты: кефир, творог, сметана и т.д.)

Механическая модель вязкой жидкости (тело Ньютона)

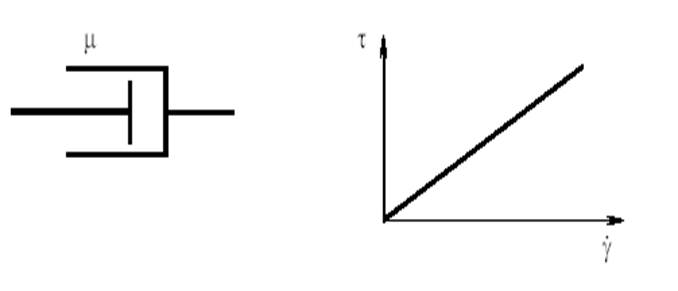
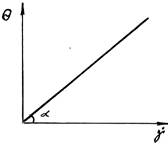Рис. 1 – Механическая модель тела Ньютона

Вязкое течение происходит под действием любых сил, как бы малы они не были, однако скорость деформации снижается при уменьшении сил, а при их исчезновении обращается в нуль. Механическая модель – демпфер, состоящий из поршня, который перемещается в цилиндре с жидкостью. При перемещении поршня жидкость через зазоры между поршнем и цилиндром протекает из одной части цилиндра в другую. При этом сопротивление перемещению поршня пропорционально его скорости.

Свойства твердых тел.

Упругость – это способность тела после деформирования полностью восстанавливать первоначальную форму или объем. Упругость тел характеризуется модулем упругости E (при растяжении, сжатии, изгибе) или G (при сдвиге), а механическое поведение упругого тела подчиняется закону Гука. Деформация объемного расширения или сжатия – изменяется объем материала, форма остается без заметных изменений. Деформация сдвига – изменяется форма материала, объем остается прежним. тело Гука является абстракцией, так как во всех реальных телах деформация протекает во времени.Твердые тела в зависимости от упругости бывают гуковскими и негуковскими. Гуковское тело – это идеально упругое тело, состояние которого описывается уравнением Гука.

θ =Gγ.

σ= ε E

θ – касательное напряжение, Па

G – модуль упругости при угловой деформации (при сдвиге), Па;

γ – угловая деформация

σ – нормальное напряжение, Па;

ε – линейная деформация

E – модуль упругости при линейной деформации (при растяжении-сжатии), Па

Механическая модель упругого твердого тела (тело Гука) - пружина

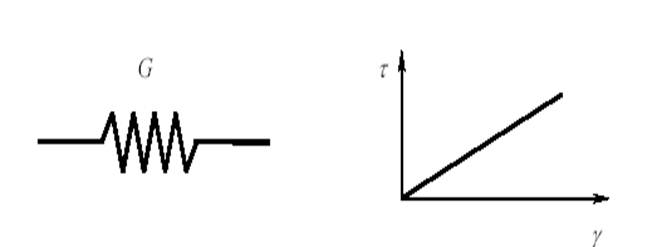
Рис. 2 - Механическая модель тела Гука

После снятия нагрузки, отдавая накопленную энергию, гуковское тело без запаздывания возвращается в исходное состояние. Для негуковского твердого тела (почти все твердые пищевые продукты) с замедленной деформацией характерно то, что при разгрузке деформация изменяется не мгновенно, а с запаздыванием, то есть наблюдается упругое последействие (т. е. медленное восстановление формы тела после снятия нагрузки), состояние равновесия достигается через определенное время, а скорость деформации является функцией времени. Энергия, затраченная на деформацию, накапливается и может быть возвращена при разгрузке

Модель идеальнопластического тела (тело Сен-Венана) – пара трения.

Пластичность – способность тела под действием внешних сил необратимо деформироваться без нарушения сплошности. Пластическое течение начинается при величине напряжений, равной пределу текучести, или при сдвиговых деформациях – при напряжении, превышающем предельное напряжение сдвига.

Тело Сен-Венана – элемент, состоящий из двух прижатых друг к другу пластин. При относительном перемещении пластин между ними возникает постоянная сила трения, не зависящая от нормальной силы. Неподатливо при нагрузке ниже предела текучести, а после его превышения неограниченно деформируется (течет).

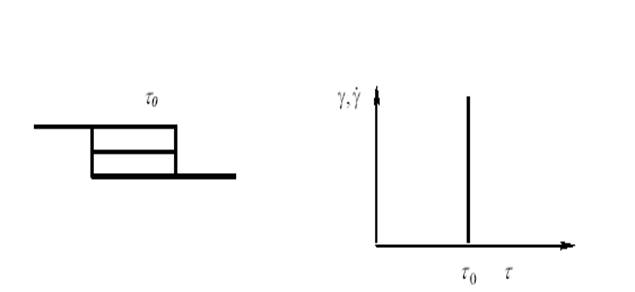
Рис. 3 - Механическая модель тела Сен-Венана

Для того чтобы описать реологическое поведение сложного тела можно комбинировать в различных сочетаниях модели простейших идеальных тел, каждое из которых обладает лишь одним физико-механическим свойством. Эти элементы могут быть скомбинированы параллельно или последовательно.

Основными сложными моделями являются:

§ упруго-пластичное тело;

§ вязко-упругое тела Кельвина-Фойгдта и Максвелла;

§ вязкопластические тела Бингама, Шведова и Шведова-Бингама.

Классификация продуктов (текстурный признак)	Наименование продуктов	Типичные реологические свойства
хрупкие, твердые	Шоколад, печенье, крекеры, вафли, карамель, сухари, сушки, макароны, хлебцы	Жесткость, предел прочности, модуль упругости
Упруго-пластичные	Хлеб, пшеничное тесто, мармелад, зефир, пастила, конфеты, твердый жир, пряники, желатин, мягкие и твердые сыры	Предел прочности, модуль упругости, предельное напряжение сдвига, адгезия
Вязко-пластичные	Ржаное тесто, песочное тесто, сметана, майонез, желирующие продукты, полуфабрикаты кондитерского производства, йогурты, творог,	Вязкость, адгезия, предельное напряжение сдвига

Модель упруго-пластического тела (рис. 1.6, а) получается при последовательном соединении упругого элемента Гука с модулем упругости G и пластического элемента Сен-Венана с пределом текучести τ _т. При τ < τ _т происходит упругая деформация материала, а при τ = τ _т – пластическое течение.

Вязко-упругое тело Кельвина – Фойгта представлено механической моделью, полученной при параллельном соединении упругого элемента Гука с модулем упругости G и вязкого элемента Ньютона с вязкостью η (рис. 1.6, б). Под действием растягивающего усилия пружина удлиняется, а поршень будет двигаться в жидкости. Это движение поршня связано с вязким сопротивлением жидкости, ввиду чего полное растяжение пружины наступает не сразу. Когда нагрузка устранена, пружина сжимается до первоначальной длины, но это требует времени вследствие вязкого сопротивления жидкости.

Для написаний математической модели тела Кельвина – Фойгта использут то обстоятельство, что при параллельном соединении элементов деформация сложного тела γ _КФ равна деформации каждого элемента, а напряжение суммарного элемента τ _КФ равно сумме напряжений в отдельных элементах τ _Г и τ _Н. На основании этого имеем систему уравнений:

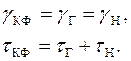(1.11)

Воспользуемся записанными ранее математическими моделями для элементов Гука (Г) и Ньютона (Н):

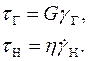(1.12)

Рассмотрев совместно (1.11) и (1.12), получим окончательно математическую реологическую модель тела Кельвина – Фойгта:

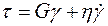, (1.13)

где: G – модуль упругости при сдвиге, Па;

γ – угловая деформация;

η – ньютоновская вязкость, Па∙с.

Рис. 1.6. Механические модели реологических материалов.

а) модель упруго-пластичного тела; б) модель Кельвина-Фойга;

в) модель Максвелла; г) модель вязко-пластического тела Шведова – Бингама; д) модель Бингама; е) модель Шведова

Модель тела Кельвина – Фойгта отражает явление упругого последействия, которое представляет собой изменение упругой деформации во времени, когда она или постоянно нарастает до некоторого предела после приложения нагрузки, или постепенно уменьшается после её снятия.

Механическая модель вязко-упругого релаксирующего тела Максвелла (рис. 1.6, в) представляет собой последовательное соединение элементов Гука с модулем упругости G и Ньютона с вязкостью η. На оба элемента действует одинаковое напряжение τ.

Тело Максвелла ведёт себя как упругое или вязкое в зависимости от отношения времени релаксации материала к длительности эксперимента. Итак, если под действием мгновенного усилия пружина растягивается, а затем сразу нагрузка снята, то поршень не успевает двигаться и система ведёт себя как упругое тело. Однако, с другой стороны, если поддерживать растяжение пружины, постоянным, она постепенно релаксирует, перемещая поршень вверх, и система ведёт себя как ньютоновская жидкость. Реологическое уравнение тела Максвелла имеет вид:

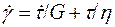. (1.14)

Двухэлементная механическая модель вязко-пластического тела Шведова – Бингама (рис. 1.6, г) состоит из соединённых параллельно элементов Ньютона с вязкостью η и Сен-Венана с пределом текучести τ _Т. Если τ ≤ τ _Т, то система ведёт себя как абсолютно твёрдое недеформированное тело. Реологическое уравнение этого тела при τ > τ _Т имеет вид:

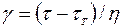. (1.15)

В природе имеются материалы, которые в первом приближении можно рассматривать как тело Сен-Венана. Они начинают течь, когда напряжение сдвига достигает предельного значения. Если нет вязкого сопротивлении, то скорость течения материала станет сколь угодно большой. Это показывает, что такие материалы могут только в первом приближении рассматриваться как тела Сен-Венана. Во втором приближении они должны обладать вязкостью. Всё это приводит к постулированию идеального тела Бингама, сочетающего упругость, вязкость и пластичность.

Механическая модель Бингама (рис. 1.6, д) состоит из элементов Гука с модулем упругости G, Ньютона с вязкостью η и Сен-Венана с пределом текучести τ _Т. Элементы Ньютона и Сен-Венана соединены взаимно параллельно, а вместе – последовательно с элементом Гука.

Под действием напряжения τ < τ _Т модель Бингама имеет только упругую деформацию. Реологическое уравнение этой модели при τ > τ _Т имеет вид:

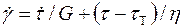. (1.16)

Механическая модель Шведова состоит из элементов Гука с модулем упругости G _Н, Сен-Венана с пределом текучести τ _Т и Максвелла с модулем упругости G _М и вязкостью η (рис. 1.6, е). В 80-х годах 19 века Ф.Н. Шведов изучил релаксационные процессы в коллоидных растворах и впервые обнаружил у них упругость и вязкость. Модель этого тела отличается от модели Бингама тем, что параллельно модели Сен-Венана присоединена модель Максвелла, а у модели Бингама – элемент Ньютона.

При τ ≤ τ _Т деформация модели Шведова происходит только благодаря элементу Гука. При τ > τ _Т деформируются все элементы модели. Реологическое уравнение модели Шведова в дифференциальной форме имеет вид:

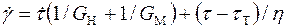. (1.17)

Стремление исследователей более точно отобразить поведение пищевых материалов под нагрузкой привело к созданию сложных моделей, что значительно увеличило трудоемкость расчетов. Модели, имеющие малое число элементов, редко дают удовлетворительную сходимость опытных данных с рассчитанными по уравнениям. В тоже время увеличение количества элементов сверх четырёх не приводит к существенному качественному изменению модели, так как модели, содержащие до четырёх элементов включительно, исчерпывают всё разнообразие механического поведения данного материала.

Представленные выше механические модели широко используются для моделирования и описания свойств реальных пищевых продуктов.

Для моделирования свойств мясных фаршей для вареных колбас рекомендуется механическая модель Шведова-Бингама (см. рис. 1.6 г). Так, например, при моделирования поведения двух и более приготовленных образцов фаршей, отличающихся хотя бы одним показателем, например вязкостью, наглядно видно, что при приложении нагрузки одной и той же величины, более существенной деформации подвергнется образец, имеющий наименьшую вязкость. А в случае, например, полной потери пластичности материал переходит в состояние вязкого материала, не способного удерживать свою форму, т.е. будет просто растекаться. С помощью данной модели можно исследовать поведение мясных фаршей например, при добавлении воды, различных добавок или оценить механическое воздействие на структуру продукта и т.д.

Для описания поведения цельной мышечной ткани мяса может применяться механическая модель Максвелла (1.6.в). Для описания других материалов могут применяться другие механические модели, рассмотренные выше.

Как показывает практика, применение механических моделей для описания поведения материалов с двумя элементами дают недостаточно точные результаты, которые могут значительно отличаться от результатов, полученных с помощью экспериментальных кривых реограмм. Поэтому с целью повышения точности предлагаются модели, состоящие из трех или четырех элементов простых моделей.

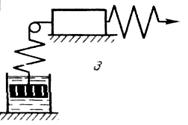
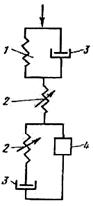
Так, например, для описания поведения материалов, обладающих одновременно упруго-пластично-вязкими свойствами, предлагается механическая модель, состоящая из двух упругих тел, пластичного и вязкого, которая представлена на рис. 2.9 а.

а б

Рис. 2.9. Механические модели реальных пищевых материалов:

а) - механическая модель продуктов типа мясных фаршей, б) – механическая модель неразрушенной мышечной ткани мяса: 1 - линейно-упругий элемент; 2 - нелинейно-упругий элемент; 3 - вязкий элемент;

4 - элемент, фиксирующий определенное значение деформации.

Данная модель более точно описывает поведение материалов типа мясные фарши, тесто и др., которые обладают одновременно тремя свойствами - упругими, пластичными и вязкими.

Для более точного описания поведения неразрушенной мышечной ткани мяса предлагается механическая модель, представленная на рис. 2.9 б.

Структура неразрушенной мышечной ткани мяса, сложная по своему строению, представлена в виде мышечных волокон, связанных пространственной соединительной пленкой. Все промежутки структуры заполнены тканевой жидкостью: слабо и сильносвязанной влагой. По характеру и прочности связи между частицами мышечную ткань можно отнести частично к конденсационно-кристаллизационным структурам. Подобные структуры обладают рядом свойств твердых тел, но в то же время эластичны, пластичны и т.д., что необходимо учитывать при выборе наиболее целесообразных способов и режимов технологической обработки.

Общая деформация механической модели складывается из нелинейно-упругой с модулем упругости 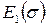(последовательно включенный элемент (2), эластичной с модулем упругости 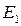и вязкостью 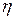₁ (параллельно соединенные элементы (1) и (3)) и пластической с нелинейным модулем упругости 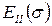, вязкостью 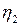и фиксатором (последовательно соединенные элементы (2), (3) и параллельно с ними фиксатор - элемент (4).

Данная механическая модель позволяет моделировать деформационные изменения мяса при осевом сжатии. Модель описывается нелинейным дифференциальным реологическим уравнением второго порядка.

Методы измерений и измерительные приборы

Для экспериментального определения реологических параметров материала или показателей консистенции существует множество методов, которые различаются по области применения (лабораторные и производственные), виду измеряемой величины (например, реологические характеристики материала и показатели консистенции), принципам нагружения, степени автоматизации и др.

Для практического выбора метода измерений учитываются необходимое количество проб, точность и продолжительность измерений и другие моменты, которые зависят от конкретных конструктивных решений измерительного прибора.

Большое число реологических методов измерения предназначено для лабораторных исследований. Кроме лабораторных методов измерений, для фундаментальных научных исследований специальных реологических характеристик материалов с высокой точностью, для многократного повторяющихся исследований предпочтение отдается тем методам и приборам, которые позволяют провести измерения и обработку их результатов быстро и с минимальной зависимостью от субъективных факторов. Промышленностью ряда стран выпускаются такие приборы, измерения на которых частично или полностью автоматизированы, а результаты обрабатываются с помощью ЭВМ. Этот аспект также оказывает заметное влияние на выбор подходящего метода измерения.

Эффективное и качественное управление процессами производства пищевых продуктов часто требует контроля реологических величин в производственных условиях. Использование лабораторных методов при этом сопряжено с большими затратами времени и труда и возможно только для очень длительных процессов. По этой причине непрерывный контроль процесса должен осуществляться с привлечением методов, которые дают измерительные сигналы постоянно или в короткие интервалы времени. Эти сигналы точно отражают реологическое состояние и обеспечивают управление процессом при отклонении от заданного режима.

Методы этого типа предусматривают использование приборов или датчиков, которые измеряют реологические свойства непосредственно в технологическом процессе. Из этих объективных условий вытекают, с одной стороны, ограничения при выборе возможного принципа измерения, с другой – требования относительно автоматизации измерений и обработки результатов, а также устойчивой и надежной работоспособности в условиях непрерывной эксплуатации. Кроме того, некоторые ограничения накладываются на точность измерения, измеряемые реологические свойства материала, температуру измерения.

Методы измерений в производственном процессе используют большей часть несложные принципы, охватывающие измерение показателей консистенции или характерных величин, которые связаны с выбранными реологическими свойствами. В особых случаях необходимо иметь в распоряжении автоматизированные методы, которые позволяют с достаточной точностью проводить измерения реологических величин.

Реологические свойства твердых пищевых продуктов можно описать в простейших случаях ньютоновской вязкостью η_н или ее функциями η(γ) или η(τ), а в сложных случаях – посредством других характеристик: предела текучести; констант, зависящих от продолжительности сдвига; вязкоупругими характеристиками. Для наиболее простой оценки измеряемой величины важно, чтобы в основе принципов нагружения (принцип нагружения устанавливает вид деформации испытуемого материала и измеряемые величины, предназначенные для обработки) лежали такие виды деформации, при которых тензоры напряжения и скорости деформации существенно упрощаются. Для определения функции течения тензор скорости деформации (скорость сдвига) необходимо измерять в максимально большом диапазоне, начиная при γ≈0.

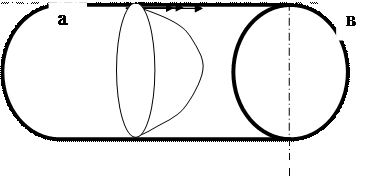
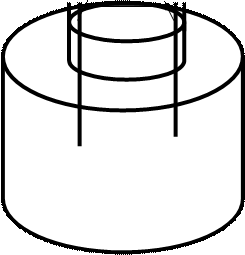
Одномерное стационарное сдвиговое течение может быть реализовано при капиллярном, плоскопараллельном цилиндрическом и торс ионном течении (см. рис. 4).

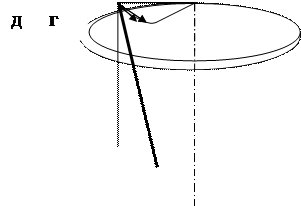Рис.4 - Виды течения при одноосном стационарном сдвиге:

а – капиллярное;

б – плоскопараллельное;

в – цилиндрическое Куэтта;

г – торсионное между двумя плоскостями;

д – торсионное между конусом и плоскостью.

Таблица 6 – Реометры одномерного сдвигового течения

Реометр	Вид течения	Область применения, требования к количеству исследуемого материала
Капиллярный вискозиметр:	капиллярное
постоянного давления	Для ньютоновских жидкостей при малых градиентах сдвига; малое количество материала
переменного давления	Для неньютоновских жидкостей в технологических процессах; большое количество материала
высокого давления	для высоковязких и пластичных сред, а также при высоких градиентах сдвига
Вискозиметр с каналом в виде щели:	Между параллельными плоскостями	Для неньютоновских жидкостей в технологических процессах; большое количество материала
широкой
кольцевой
Ротационный вискозиметр
с соосными цилиндрами	Цилиндрическое Куэтта	Для ньютоновских и неньютоновских жидкостей в качестве лабораторных приборов; малое количество материала
с параллельными плоскостями	Торсионное
типа конус - плоскость	Торсионное между конусом и пластиной	Для ньютоновских и неньютоновских жидкостей при постоянном градиенте сдвига в измерительном зазоре; очень малое количество материала
типа сфера - сфера	Торсионное между шаром и сферической оболочкой	Для ньютоновских и неньютоновских жидкостей в качестве лабораторных приборов; малое количество материала

Известны реометры, принцип измерений которых основан на течение Стокса вокруг падающих шариков (см. табл. 7).

Таблица 7 – Реометры течения Стокса

Реометр	Вид течения	Область применения
Вискозиметр с падающим шариком и широкой трубкой	Стокса вокруг шарика	для ньютоновских жидкостей с использованием различных шариков; для неньютоновских жидкостей применение ограничено
Вискозиметр с падающим шариком и узкой трубкой	Модифицированное Стокса около шарика в кольцевом зазоре	для прозрачных ньютоновских жидкостей; для лабораторных приборов
Вискозиметр с толкаемым шариком и узкой трубкой	для ньютоновских и неньютоновских жидкостей; для лабораторных приборов

Расчет скорости сдвига для падающих шариков в узкой трубе чрезвычайно сложен, поэтому константы прибора определяют посредством калибровки с помощью жидкости с известной вязкостью.

Для качественного определения вязкоупругих характеристик используют реометры, основанные на одномерном осциллирующем сдвиговом течении (см. табл. 8).

Таблица 8 – Реометры одномерного осциллирующего сдвигового течения

Тип колебаний	Рабочие органы реометра	Область применения
Вынужденные вращательные с малой амплитудой и переменной частотой	Плоскость – плоскость, конус – плоскость, коаксиальные цилиндры	Для количественного определения динамических модулей и постоянных времени вязкоупругих жидкостей
Свободные вращательные с начальными условиями	Для определения реологических характеристик вязкоупругих жидкостей
Вынужденные за счет эксцентриситета оси вращения	Плоскость – плоскость, эксцентричные цилиндры	Для количественного определения динамических модулей и постоянных времени вязкоупругих жидкостей
Вынужденные из-за относительного отклонения оси вращения	Полусфера – полусферическая оболочка, конус – плоскость, цилиндр – цилиндр

Влияние вибрации на изменение структуры неньютоновских жидкостей, которое приводит к уменьшению эффективной вязкости предела текучести, исследуют с помощью одномерного сдвигового течения в соосных цилиндрах с наложением вибрации.

Для исследования консистенции сложных неньютоновских жидкостей применяют методы, которые обеспечивают быстрые, воспроизводимые результаты измерения. Такие методы приобретают особое значение при исследовании пищевых продуктов или полуфабрикатов, реологические свойства которых быстро изменяются вследствие ферментативных, химических или физических процессов. Методы этого типа базируются на таких принципах нагружения, которые подходят для оценки характерных реологических свойств или параметров текстуры (см. табл.9). При этом получают характеристические кривые или характеристические параметры, которые выражаются в относительных единицах.

Таблица 9 – Методы определения консистенции и реологических характеристик материалов в основе комплексного нагружения.

Принцип нагружения	Измеряемая величина	Область применения
Внедрение индентора определенной формы и размеров при заданном усилии и времени внедрения; типичные формы инденторов – конус, шар, полушар, цилиндрический штифт, игла	Глубина внедрения по истечении определенного времени; глубина внедрения в равновесном состоянии; кинетика внедрения в течение всего времени измерения	Для пластичных и упругопластичных материалов, таких, как мягкие жиры, тесто, желе, пасты в статическом состоянии
Перемешивание жидкости при определенных траекториях движения, геометрии сосуда, количестве и температуре материала и определенной частоте вращения	крутящий момент	Для жидких и вязких суспензий, эмульсий пенообразных масс с малым пределом текучести или при его отсутствии
Замес вязких масс и теста в определенном месильном устройстве при определенных геометрии месильной камеры, количестве и температуре материала, частоте вращения	Для вязких масс и теста; для процесса тестообразования; для процессов изменения структуры при механическом нагружении или введении добавок
Экструдирование пластичных масс через узкие отверстия определенной геометрии при постоянных скорости экструдирования и температуре	Давление при определенной скорости экструдирования; количество экструдируемого материала	для пластичных и упругопластичных масс в динамическом состоянии
Падение тела определенной геометрической формы на определенном отрезке специальной трубы, наполненной вязкой жидкостью с заданной температурой	Время падения	Для вязких растворов или суспензий с частицами грубодисперсных компонентов
Колебательное нагружение с определенной амплитудой и частотой	Затухание колебаний; резонансная частота
Растекание вязкой или вязкоупругой массы определенного количества и первоначальной формы при постоянной температуре под действием сил тяжести	Уменьшение высоты; увеличение площади	Для малого количества вязких или вязкоупругих масс

Реологические свойства твердых пищевых продуктов значительно сложнее, чем жидкостей, и только в простейших случаях гуковского тела описываются посредством модуля Юнга Е, модуля сдвига G, модуля объемной упругости Е_υ и коэффициента Пуассона.

Для негуковских тел характерны более сложные параметры, которые можно описать благодаря другим характеристикам, таким, как предел текучести, вязкость, период релаксации, период упругого последействия (ретардации).

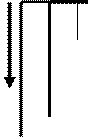
При исследовании твердых пищевых продуктов также используют принципы нагружения, при которых тензоры напряжения, деформации и скорости деформации существенно упрощаются. К ним относятся одноосное сжатие или растяжение, простой сдвиг между параллельными плоскостями, кручение цилиндрического стержня и изотропное сжатие (см. рис 5). При исследовании вязкоупругих пищевых продуктов необходимо учитывать влияние температуры, скорости деформации и кинетики нагружения. Область малых деформаций при измерении, как правило, превышается. Предел текучести и предел прочности имеют динамический характер.

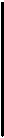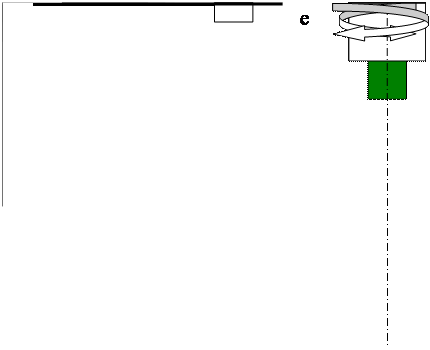Рис. 5 – Принципы нагружения твердых тел:

а – одностороннее сжатие;

б – одноосное растяжение;

в – одноосный сдвиг;

г – кручение;

д – всестороннее сжатие при двумерной компрессии;

е – всестороннее (гидростатическое) давление.

При постоянной скорости нагружения получают зависимость между напряжением и деформацией, которая для вязкоупругих твердых тел является функцией скорости деформации. Вычисленные при этом характеристики называются “кажущимися”, или эффективными, так как они имеют значение только для определенной скорости нагружения.

Нагружение с постоянной скоростью деформации и внезапной остановкой ниже предела прочности используют для изучения релаксации напряжений.

При постоянном напряжении получают кривые, изменяющиеся во времени деформации (кинетику деформации). Постепенно повышая напряжение после достижения состояния равновесия, получают семейство кривых кинетики деформации. Обрабатывая эти кривые, получают математическую модель и определяют константы материала.

При очень сложных реологических свойствах твердых тел, особенно при наличии анизотропных структурных элементов (поры, волокна), только с помощью параметров текстуры или показателей консистенции. Для этого наряду с обычными принципами измерения для твердых пищевых продуктов применяются такие, которые имитируют или типичные механические процессы при переработке материалов, или нагружение продуктов питания при потреблении. Сюда относятся раздавливание, резание, сжатие. см. табл.10

Таблица 10 – Принципы измерений для определения характеристик консистенции или параметров текстуры твердых пищевых продуктов

Принцип измерения	Измеряемая величина
Сжатие образца заданных размеров и формы между двумя параллельными пластинами при постоянной нагрузке или постоянной скорости смещения пластин	Относительное сжатие через определенное время, а также в равновесном состоянии; сжимающее усилие при заданном относительном сжатии; максимальное сжимающее усилие, характерные величины кривой сжатия; полная кривая сжатия
Сплющивание между двумя рабочими органами определенных размеров и формы при постоянной скорости смещения рабочих органов	Максимальная сила сплющивания; полная кривая сплющивания
Резание образца струной или ножом с постоянной скоростью	Сила при внедрении режущего инструмента
Срез плоского образца между верхним и нижним лезвием	Сила среза

Для инструментального определения твердости как сопротивления пластичному проникновению более твердого тела используют инденторы круглой, конусообразной или пирамидальной формы, которые вдавливают в исследуемые материалы. Вследствие анизотропных свойств пищевых материалов твердость зависит от места нагружения, так что следует различать микротвердость и макротвердость. Для определения микротвердости применяют инденторы конусообразной или пирамидальной формы. Макротвердость является средней твердостью больших по площади образцов. Для ее измерения более подходят тела круглой формы. Показатели твердости определяются при остаточной деформации отпечатка при определенных размерах индентора, нагружающей силе, а также скорости деформации. Вследствие относительного характера измерения твердости сравнивать результаты измерения у различных продуктов можно только в том случае, когда используются одинаковые методы.

Внешнее трение зависит от скорости поверхностей тел, находящихся в контакте (в свою очередь, зависит от шероховатости), твердости и силы прижатия тел одного к другому. Принцип измерения при определении коэффициента трения основан на установлении силы, которая необходима для передвижения исследуемого тела с определенной поверхностью и силой прижатия по другой поверхности. Противоположная поверхность съемна, чтобы могли исследоваться различные материалы.

Принцип измерения адгезии и склеивающей способности основаны на определении силы, необходимой для отделения контактной поверхности от прилипшего материала. Для этого между двумя одинаковыми поверхностями помещают исследуемый материал и плотно их прижимают. Отделяют их посредством нормального или тангенциального усилия. Если испытуемый материал полностью отделяется от контактных поверхностей, речь идет об адгезии. Толщина слоя испытуемого материала в этом случае не оказывает влияния на результат измерения. Если после разделения поверхностей испытуемый материал частично остается на поверхности контакта, отделение происходит посредством преодоления адгезии и когезии и речь идет об измерении склеивающей способности. В этом случае толщина слоя испытуемого материала влияет на результаты измерений и должна учитываться в исследованиях. Укрупненная классификация приборов, предназначенных для исследования описанных выше структурно-механических свойств и текстуры пищевых продуктов и полуфабрикатов приведена в табл. 11.

Таблица 11 – Классификация реометров

Реометры	Вид нагружения (течения)	Измеряемая величина	Область применения
Вискозиметры	капиллярные	Одномерное сдвиговое течение	Реологические характеристики	Фруктовые и овощные соки, молоко, кефир, сливки, растительное масло, сиропы, творог, мясной и рыбный фарши; пасты конфетные массы, тесто,
ротационные
шариковые	Течение Стокса
колебательные	Одномерное и двумерное сдвиговое течение
Пенетрометры	Многомерное пенетрационное течение	Предельное напряжение сдвига, параметры текстуры	Твердые жиры, желе, тесто, мякиш хлеба, фрукты, овощи, сыр, колбаса, мясо, шоколад
Компрессионные приборы	сжатие образца	Предел прочности при сжатии, объемная вязкость, параметры текстуры	Твердообразные пищевые продукты
Универсальные приборы типа “Инстрон”	Растяжение, сжатие, изгиб, сдвиг и другие простейшие виды нагружения исследуемого продукта	Прочностные характеристики, параметры текстуры
Трибометры	Сдвиг	Фрикционные характеристики
Адгезиометры	Отрыв контактирующего элемента от поверхности исследуемого материала	Адгезионные характеристики

Физико-механические свойства материалов

Твердость – это комплексное свойство негуковских тел оказывать сопротивление проникновению другого тела вследствие необратимых (упругой и вязкой) деформаций. При негомогенном структурном строении тел микротвердость в различных телах неодинакова. Вследствие этого прямой зависимости между твердостью и прочностью не существует.

твердость нельзя выразить как физическую величину с однозначной размерностью. Она является некоторым техническим параметром, который выражается в относительных величинах в зависимости от метода определения.

Твердость определяется следующими методами: Нанесение царапин (шкала твердости по Мосу); внедрение в исследуемое тело более твердого тела, например шара (твердость по Бринелю); конуса (твердость по Роквеллу), пирамиды (твердость по Викерсу).

Коэффициент твердости рассчитывают по величине силы и геометрическим параметрам остаточной деформации (шарового сегмента, глубины внедрения). Между коэффициентами твердости, полученными с помощью различных методов, существуют определенные соотношения.

Мягкость – свойство, противоположное твердости.

Хрупкость – свойство твердых тел достигать разрушения без пластичной деформации. Чисто гуковские тела обнаруживают хрупкое разрушение при любой скорости деформации. У негуковских тел хрупкое разрушение наступает только при высоких скоростях деформации или низких температурах, когда теряют действие вязкие свойства.

Когезия – сопротивление тел разрушению, связанному с преодолением сил взаимодействия между атомами и молекулами на поверхности раздела. Между работой когезии и работой хрупкого разрушения существует прямая зависимость.

Адгезия – свойство, которое основывается на взаимодействии двух различных тел на границе раздела фаз и вызывает сцепление тел. При разделении тел необходимо преодолеть силы сцепления. Прочность соединения двух тел из различных материалов зависит от площади и состояния поверхности контакта между телами.

Липкость – свойство пограничного слоя вязких или пластичных материалов оказывать сопротивление разделению находящихся в контакте с поверхностью. Оно основывается на адгезии материалов, на поверхности раздела и когезии самого испытуемого материала. Если силы когезии больше, чем силы адгезии, разделение происходит в результате преодоления сил адгезии, и наоборот. Если обе силы приблизительно равны, разделение происходит благодаря частичному преодолению сил когезии и адгезии.

Внешнее трение – сопротивление относительному перемещению двух находящихся в соприкосновении поверхностей твердого тела. Для начала скольжения необходимо приложить нагрузку, превышающую силы трения покоя.