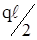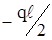Рис.5.4
Дифференциальные и интегральные зависимости между q, Q и M
Установим некоторые зависимости, знание которых облегчит построение эпюр и даёт возможность в известной мере контролировать их правильность.
Рассмотрим балку с произвольной нагрузкой (рис.5.4,а).
а б
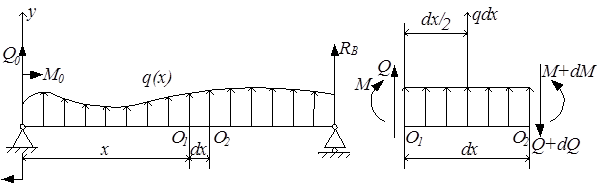
Выделим малый элемент балки O1O2 длиной dx и рассмотрим его равновесие (рис.5.4,б). В пределах малого участка распределённую нагрузку можно считать постоянной q (x) = const = q. Поскольку в общем случае Q и M меняются вдоль оси балки, в сечении O1 будем иметь Q(x) и M(x), а в сечении O2: Q(x) + dQ(x) и M(x) + dM(x). Как всегда, изображаем их положительно направленными. Из условия равновесия элемента O1O2 получим:
∑y = 0: Q + qdx – (Q + dQ) = 0,
∑M02 = 0: 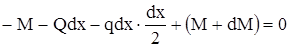
Первое уравнение даёт условие
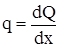 . (5.3)
. (5.3)
Из второго уравнения, пренебрегая членом 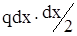 , найдём:
, найдём:
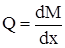 . (5.4)
. (5.4)
Из формул (5.3) и (5.4) следует, что
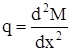 . (5.5)
. (5.5)
Выражения (5.3) – (5.5) называют дифференциальными зависимостями при изгибе. Из них можно получить интегральные зависимости
Q = ∫qdx + Q0, (5.6)
M = ∫Qdx + M0. (5.7)
где Q0 и M0 - постоянные интегрирования (значения сосредоточенной силы и сосредоточенного момента в начале участка).
Использование интегральных зависимостей позволит упростить и ускорить построение эпюр.
Рассмотрим порядок построения эпюр Q и M для наиболее характерных, часто встречающихся случаев нагружения балок.
Сосредоточенная сила на свободном конце консоли (рис.5.5).
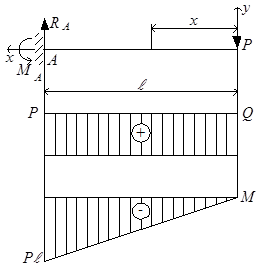 Рис.5.5
Рис.5.5
| 0 ≤ x ≤ ℓ
Q(x) = P
M(x) = – Px
Балка имеет один участок. Начало координат выбираем в крайней правой точке, ось x направляем влево. При такой системе координат можно не находить реакции опоры. Вычисляем Q и M в произвольном сечении участка с абсциссой x. Для построения графиков достаточно получить две точки – в начале и в конце участка. Эти вычисления удобно делать в табличной форме. |
Как видно из уравнений и из графиков, Q – постоянная, M – линейная функция. Для расчётов на прочность важно знать наибольшее значение изгибающего момента. В данном случае |Mmax| = Pℓ. По эпюрам можно определить опорные реакции: RA = P, MA = – Pℓ.
Двухопорная балка с сосредоточенной силой посередине (рис.5.6).
Прежде всего найдём опорные реакции:
∑MA = 0: 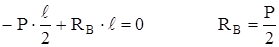 ,
,
∑y = 0: 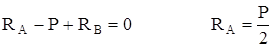 .
.
В данном случае имеем на балке два участка. Для первого будем отсчитывать x от левой опоры А, для второго – от правой опоры В. Запишем уравнения Q и M, вычислим их значения на границах участков и построим эпюры
0 ≤ x1 ≤ ℓ/2,
Q(x) = RA = P/2,
M(x) = RA ∙ x = P/2 ∙ x.
0 ≤ x2 ≤ ℓ/2, Q(x) = – RВ = – P/2, M(x) = RВ ∙ x = P/2 ∙ x Mmax = Pℓ/4.
|  Рис.5.6
Рис.5.6
|
Консольная балка с равномерно распределённой нагрузкой (Рис.5.7). Балка имеет один участок. По аналогии с балкой на рис.5.5 отсчитываем x от свободного конца балки и поэтому не определяем опорные реакции.
|
0 ≤ x ≤ ℓ, Q(x) = q ∙ x, M(x) = – qx2/2.
Как видно из уравнений: Q – линейная функция, M – квадратная парабола.
|  Рис.5.7
Рис.5.7
|
Двухопорная балка с равномерно распределённой нагрузкой (рис.5.8). В данном случае необходимо сначала определить опорные реакции
∑МА = 0: 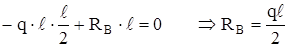 ,
,
∑у = 0: 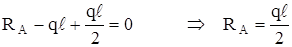 .
.
При подсчете момента от распределённой нагрузки мы заменяем её статическим эквивалентом – равнодействующей, и мысленно прикладываем эту равнодействующую в центре тяжести распределённой нагрузки. Затем определяем момент как произведение силы на плечо (рис.5.5,б). В нашем случае равнодействующая равна qℓ и приложена она должна быть в середине балки – на расстоянии ℓ/2 от опоры A.
 Рис.5.8
Рис.5.8
| 0 ≤ x ≤ ℓ
Из уравнений следует, что Q – линейная функция, M – квадратная парабола. Также видно, что в соответствии с формулой (5.4) Q – производная от M. В точке, где производная равна нулю, функция имеет экстремум. |
Найдём его
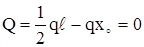 , х0 = ℓ/2,
, х0 = ℓ/2, 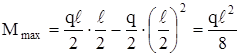 .
.
Получили, что в середине пролёта имеет место максимальный изгиб. момент.
Двухопорная балка со сосредоточенным моментом на опоре (рис.5.9). Находим опорные реакции, направив их вверх.
 Рис.5.9
Рис.5.9
| ∑MA = 0: M + RB ∙ ℓ = 0, 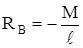 ,
∑y = 0: RA + RB = 0, ,
∑y = 0: RA + RB = 0, 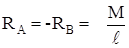 .
Меняем направление RB на обратное.0 ≤ x ≤ ℓ .
Меняем направление RB на обратное.0 ≤ x ≤ ℓ
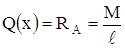 , ,
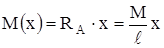 .
По уравнениям строим графики. .
По уравнениям строим графики.
|
Двухопорная балка с симметричными консолями (рис.5.10). Ввиду симметрии балки и нагрузки реакции опор направлены вверх и каждая из них равна Р. У балки три участка.
| 0 ≤ x1 ≤ ℓ Q(x) = – P, M(x) = – Px, 0 ≤ x2 ≤ ℓ Q(x) = P, M(x) = – Px, ℓ ≤ x3 ≤ 3ℓ Q(x) = – P + RA = – P + P = 0, M(x) = – Px + RA(x - ℓ) = – Px + Px – Pℓ = – Pℓ. На участке между опорами имеет место так называемый чистый изгиб – M = const, Q = 0. Рассмотрев примеры простых, «табличных» балок, перейдём к балке с произвольной нагрузкой. | 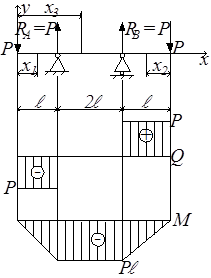 Рис.5.10
Рис.5.10
|
Двухопорная балка с консолью и тремя участками (рис.5.11). Находим опорные реакции.
∑MA = 0: – q ∙ 3 ∙ 1,5 + M + 4,5 RB – P ∙ 6 = 0,
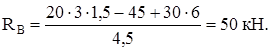
∑y = 0: RA – q ∙ 3 + RB – P = 0 Þ RA = 20 ∙ 3 – 50 + 30 = 40 кН.
0 ≤ x1 ≤ 1,5 Q(x) = P = 30, M(x) = – Px = – 30х.
1,5 ≤ x2 ≤ 3 Q(x) = P – RB = 30 – 50 = – 20, M(x) = – Px + RB ∙ (x – 1,5) = = – 30х + 50x – 75 = 20x – 75.
|  Рис.5.11
Рис.5.11
|
0 ≤ x3 ≤ 3
Q(x) = P – qx = 40 – 20x,
M(x) = – RA ∙ x – ½ qx2 = 40х – 10x2.
| x | ||
| Q | – 20 | |
| M |
На третьем участке, в точке, где график Q пересекает ноль, имеет место экстремум изгибающего момента.
Найдём его
Q = 40 – 20x0 = 0 Þ x0 = 2м,
Mmax = 40 ∙ 2 – 10 ∙ 22 = 40 кН∙м.
Анализ приведённых примеров и зависимости п.5.2 позволяет установить некоторые особенности эпюр поперечных сил и изгибающих моментов.
1. Участок балки – это часть её, в пределах которой функции Q и M непрерывны. Участок ограничен сосредоточенными силами или моментами, а также началом и концом распределённой нагрузки.
2. На участках, где нет распределённой нагрузки, поперечная сила Q постоянна, а изгибающий момент M меняется по линейному закону.
3. На участках, где к балке приложена равномерно распределённая нагрузка q, поперечная сила Q меняется по линейному закону, а изгибающий момент M – по закону квадратной параболы. В случае приложения распределённой нагрузки q, меняющейся по линейному закону (гидростатического давления), Q будет меняться по квадратной параболе, а M – по кубической параболе.
4. Изгибающий момент достигает максимума или минимума в сечениях, в которых график Q пересекает нулевую (базисную) линию. При этом выпуклость параболы обращена в сторону, противоположную направлению действия нагрузки q – правило “зонтика” (рис.5.12).
5. На участках, где Q = 0, M = const– имеет место чистый изгиб.
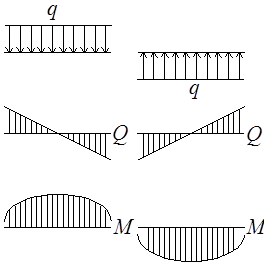 Рис.5.12
Рис.5.12
| 6. При движении по балке слева направо на участках, где Q > 0, изгибающий момент M возрастает; на участках, где Q < 0, M – убывает. 7. В сечениях, где к балке приложены сосредоточенные силы, на эпюре Q будут скачки на величину и в направлении приложенных сил, а на эпюре M будут переломы, причем остриё перелома направлено против действия силы. 8. В сечениях, где к балке приложены сосредоточенные моменты, на эпюре M будут скачки на величину этих моментов (на эпюре Q изменений не будет). Направление скачка зависит от направления внешнего момента. |
Порядок построения эпюр Q и M.
1. Составляются уравнения статики, из которых определяются величины и направления опорных реакций.
2. Балка разбивается на участки.
3. Для каждого участка составляются аналитические выражения поперечных сил Q(x) и изгибающихся моментов M(x).
4. По полученным выражениям вычисляются ординаты эпюр на границах участков.
5. Определяются сечения, в которых действуют моменты Mmax и Mmin, и вычисляются значения этих моментов.
6. По ординатам и формулам строятся эпюры.
При наличии некоторого навыка построения эпюр описанный выше алгоритм можно упростить – не составлять аналитических выражений Q и M. После определения реакций строится эпюра Q по легко вычисляемым значениям на границах участков. Затем в характерных точках вычисляются значения M как площадь предшествующей эпюры Q – см. формулу (5.7). При этом для вычисления Mmax необходимо определить площадь треугольника на эпюре Q: один катет его известен – это значение Q, другой – х0 находится очень просто х0 = Q/q.
 2014-02-24
2014-02-24 4979
4979

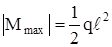 .
.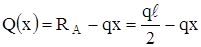 ,
,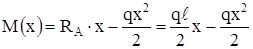 .
.