Они определяются по формулам

W_K = ahb², (7.21)

J_K = βhb³, (7.22)

где h – длинная сторона прямоугольного сечения;

b – короткая его сторона;

a и b - коэффициенты, зависящие от отношения h/b, приводятся в справочниках.

Распределение касательных напряжений в прямоугольном сечении показано на рис.7.13,б. Наибольшие напряжения, определяемые по формуле (7.19), возникают у поверхности посередине длинных сторон (в точках B и D).

Напряжения, возникающие у поверхности сечения посередине коротких сторон, (в точках A и С) меньше, они определяются по формуле

τ = γ ∙ τ_max. (7.23)

В углах и в центре напряжения равны нулю.

7.6. Расчёт цилиндрических винтовых пружин с малым шагом

В технике широко применяются пружины различных типов. Наибольшее распространение имеют цилиндрические винтовые пружины растяжения – сжатия с малым шагом, то есть с малым углом наклона проволоки (рис. 7.14,а).

Обозначим:

D = 2R– средний диаметр пружины;

d = 2r – диаметр проволоки;

n – число рабочих витков;

λ – осадка пружины.

Пусть пружина подвергается растяжению центрально приложенной силой Р.

Чтобы установить расчётные формулы для напряжений, разрежем её мысленно на две части по любому витку плоскостью, перпендикулярной оси витка. Удаляя нижнюю часть пружины, рассмотрим условие равновесия оставшейся (верхней) её части (рис. 7.14,в). Угол наклона витка a не превышает 8 – 10°, т.к. пружина с малым шагом. Поэтому можно считать cos a» 1 и sin a» 0 и пренебречь нормальной силой N и изгибающим моментом; поперечная сила Q = P (рис. 7.14,б). Очевидно, влияние отброшенной части на рассматриваемую может быть учтено приложением к месту разреза витка поперечной силы

Q = P

и крутящего момента

M_кр = PR.

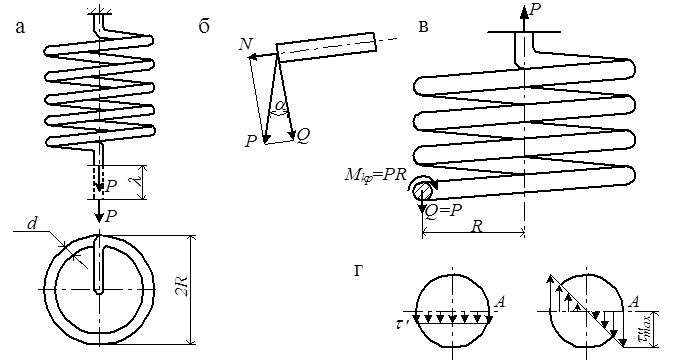
Рис. 7.14

Таким образом, в сечении пружины имеется две группы касательных напряжений (рис.7.14,г):

1) напряжения от среза, равномерно распределённые по сечению

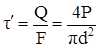; (7.24)

2) напряжения от кручения, максимальное значение которых

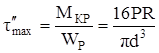. (7.25)

Как видно из картины распределения напряжений, в точке сечения витка на внутреннем радиусе (в точке А) касательные напряжения τ′ и τ′′ совпадают по направлению. Поэтому максимальные напряжения в пружине

,

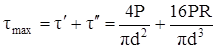или

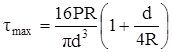. (7.26)

В большинстве случаев расчёта пружины 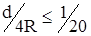(проволока относительно тонкая) и скобка в формуле (7.26) становится равной единице. Тогда условие прочности пружины будет

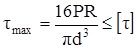. (7.27)

Напряжения от среза следует учитывать при расчёте “толстых” пружин, таких, например, как применяемых в подвеске железнодорожных вагонов.

Пружины должны сочетать прочность с большой деформативностью, поэтому они изготовляются из высокопрочных материалов с обязательной термообработкой. Величина [τ] зависит не только от материала, но и от диаметра проволоки: чем он меньше, тем [τ] больше. Так, для закалённой пружинной стали [t] = 35 – 50 кН/см² (d = 12 – 6 мм); для хромоникелевых сталей [t] = 70 кН/см² (d = 12 – 6 мм).

Для определения осадки пружины λ (взаимного перемещения её торцов вдоль оси) воспользуемся энергетическим методом. Сила Р совершает работу на перемещении λ. Так как зависимость между ними линейная, эта работа будет равна

A = ½ Pλ.

В пружине, работающей на кручение, накапливается энергия деформации, которую можно найти по формуле (7.18). При этом M_кр = PR, l = 2pRn – длина пружинной проволоки, J_P = pd⁴/32 = pr⁴/2. Получим

.

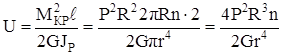Приравняв работу внешней силы и потенциальную энергию упругой деформации, получим формулу для λ:

,

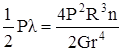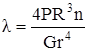. (7.28)

В заключение отметим, что кроме рассмотренных цилиндрических пружин постоянного сечения с пологим наклоном витка, существует целый ряд других конструкций: конические, призматические, фасонные (параболические, двойные, конические, бочкообразные). При этом шаг пружины может быть как постоянным, так и переменным, а сечение витка не только круглой, но и прямоугольной формы. Характеристика таких пружин, как правило, нелинейная, а методы расчёта довольно сложны, и здесь не рассматриваются.