2014-02-24
867
1. 
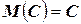, где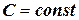 
;
2. 
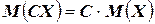- постоянный множитель можно выносить за знак математического ожидания;
3. 
;
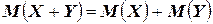4. 
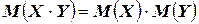, где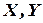 
- независимые случайные величины (если закон распределения одной из них не зависит от того, какие возможные значения приняла другая случайная величина).
Модой дискретной случайной величины называется её наибольшее вероятное значение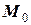 
.
Модой непрерывной случайной величины называется такое её значение 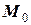, при котором плотность распределения имеет максимум, т.е.
.
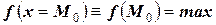Геометрически, мода – это абсцисса точки максимума кривой распределения случайной величины.
Медианой случайной величины называется такое её значение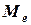 
, относительно которого равновероятно, что данная случайная величина окажется больше или меньше медианы, т.е.
.
|
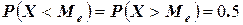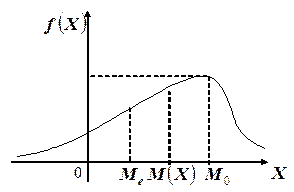
Геометрически, медиана – это абсцисса точки, в которой площадь области, ограниченная кривой распределения и осью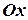 
, делится пополам.
Если распределение симметрично и имеет один максимум, то все три указанные характеристики совпадают. На рисунке изображён случай несимметричного распределения случайной величины.
