I. Закон распределения вероятностей дискретной случайной величины
На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все её возможные значения. В действительности это не так: различные случайные величины иногда могут иметь одинаковые перечни возможных значений, а соответствующие вероятности этих значений – различные. Поэтому для полной характеристики мало знать значения случайной величины, нужно ещё знать, как часто эти значения встречаются в опыте при его повторении, т.е. нужно ещё указать вероятности их появления.
Рассмотрим случайную величину 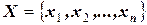 . Появление каждого их возможных значений
. Появление каждого их возможных значений 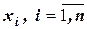 свидетельствует о том, что произошло соответственно одно из событий
свидетельствует о том, что произошло соответственно одно из событий 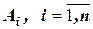 , которые образуют полную группу[5]. Допустим, что вероятности этих событий
, которые образуют полную группу[5]. Допустим, что вероятности этих событий 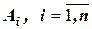 известны:
известны:
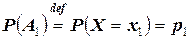 ,...,
,..., 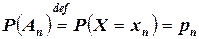 ,
,
причём 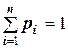 .
.
Тогда: соответствие, устанавливающее связь между возможными значениями случайной величины и их вероятностями, называется законом распределения вероятностей случайной величины, или просто – законом распределения случайной величины.
Закон распределения вероятностей данной случайной величины можно задать таблично (ряд распределения), аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности, т.е.

| 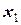
| 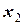
| ... | 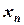
| |
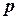
|
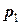
|
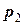
| ... |
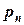
| 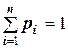
|
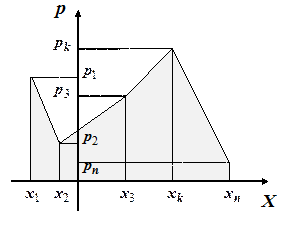
В целях наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки 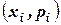 , а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения. При этом, сумма ординат
, а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения. При этом, сумма ординат 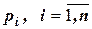 построенного многоугольника равна единице.
построенного многоугольника равна единице.
Аналитически закон распределения дискретной случайной величины можно записать, например, используя формулу Бернулли для схемы повторения независимых опытов. Так, если обозначить случайную величину, которой является число бракованных деталей в выборке, через  , то возможные её значения
, то возможные её значения 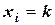 будут 0, 1, 2,...,
будут 0, 1, 2,..., 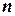 . Тогда, очевидно, формула Бернулли будет устанавливать зависимость между значениями
. Тогда, очевидно, формула Бернулли будет устанавливать зависимость между значениями 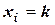 и вероятностью
и вероятностью 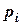 (
(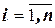 ) их появления, где
) их появления, где
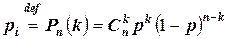 ,
,
что о определяет закон распределения данной случайной величины.
II. Закон распределения вероятностей непрерывной случайной величины
Вспомним, что дискретная случайная величина задаётся перечнем всех её возможных значений и их вероятностей. Такой способ задания не является общим: он не применим, например, для непрерывных случайных величин.
Действительно, рассмотрим случайную величину  , возможные значения которой сплошь заполняют интервал
, возможные значения которой сплошь заполняют интервал  . Можно ли составить перечень всех возможных значений
. Можно ли составить перечень всех возможных значений  ? Очевидно, что этого сделать нельзя. Этот пример указывает на целесообразность дать общий способ задания любых типов случайных величин (как уже отмечалось, дискретная случайная величина является частным случаем непрерывной случайной величины). С этой целью вводят интегральную функцию распределения.
? Очевидно, что этого сделать нельзя. Этот пример указывает на целесообразность дать общий способ задания любых типов случайных величин (как уже отмечалось, дискретная случайная величина является частным случаем непрерывной случайной величины). С этой целью вводят интегральную функцию распределения.
Пусть 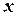 – переменная, принимающая произвольные действительные значения (на оси
– переменная, принимающая произвольные действительные значения (на оси 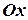 :
: 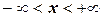 ). Рассмотрим событие
). Рассмотрим событие  , состоящее в том, что случайная величина
, состоящее в том, что случайная величина  примет значение меньшее
примет значение меньшее 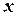 . Тогда, вероятность
. Тогда, вероятность 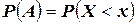 события
события  зависит от
зависит от 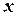 , т.е. является функцией от
, т.е. является функцией от 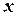 . Эту функцию принято обозначать через
. Эту функцию принято обозначать через 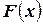 и называть функцией распределения случайной величины или, ещё – интегральной функцией распределения. Другими словами:
и называть функцией распределения случайной величины или, ещё – интегральной функцией распределения. Другими словами:
интегральной функцией распределения называют функцию 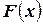 , определяющую для каждого значения
, определяющую для каждого значения 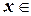 R вероятность того, что случайная величина
R вероятность того, что случайная величина  примет значение, меньшее
примет значение, меньшее 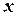 , т.е.
, т.е.
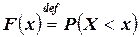 .
.
Геометрически это равенство можно истолковывать так: 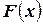 есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки
есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки 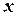 .
.
Свойства интегральной функции 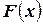 :
:
1. Значения интегральной функции принадлежат отрезку 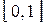 , т.е.
, т.е.
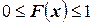 .
.
Доказательство этого свойства вытекает из определения интегральной функции как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.
2. 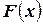 - неубывающая функция, т.е.
- неубывающая функция, т.е. 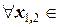 R |
R | 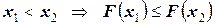 .
.
Действительно, пусть  – событие, состоящее в том, что случайная величина
– событие, состоящее в том, что случайная величина  примет значение меньшее
примет значение меньшее 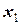 ; аналогично,
; аналогично, 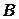 – событие, состоящее в том, что случайная величина
– событие, состоящее в том, что случайная величина  примет значение меньшее
примет значение меньшее 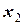 . Другими словами:
. Другими словами:
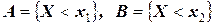
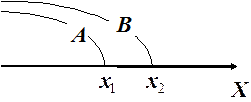
|
Следовательно, если 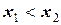 , то
, то 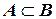 . Значит (объяснить - почему?)
. Значит (объяснить - почему?) 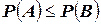 или, что то же самое:
или, что то же самое:
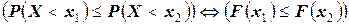 .
.
Что и требовалось показать.
3. Если возможные значения непрерывной случайной величины расположены на всей числовой оси  , то справедливо следующее предельное соотношение:
, то справедливо следующее предельное соотношение:
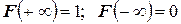 .
.
Это свойство вполне очевидно. Так, если 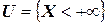 - достоверное событие, а
- достоверное событие, а 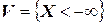 – невозможное событие, то
– невозможное событие, то
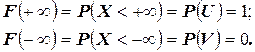
4. Вероятность того, что случайная величина примет значение, заключенное в интервале  , равна приращению интегральной функции на этом интервале:
, равна приращению интегральной функции на этом интервале:
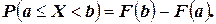
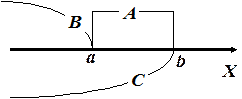
|
Рассмотрим следующие события: 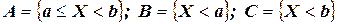 . Видим, что
. Видим, что 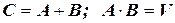 – т.е. события
– т.е. события  и
и 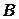 несовместны. Тогда
несовместны. Тогда
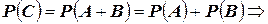
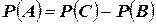 .
.
Но 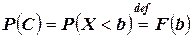 ,
,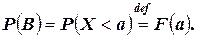 В результате, можем записать:
В результате, можем записать: 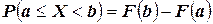 , что и требовалось показать.
, что и требовалось показать.
Мы будем в основном изучать такие непрерывные случайные величины, функции распределения которых непрерывны.
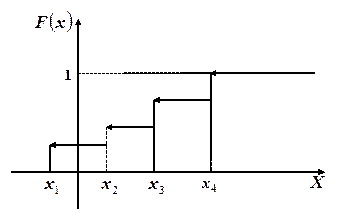
|
График функция распределения дискретной случайной величины представляет собой ступенчатую ломаную линию (см. рис.). Величина скачка в точках разрыва равна вероятности значения случайной величины в этой точке. Зная ряд распределения случайной величины, можно построить график её функции распределения:
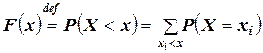 .
.
Для непрерывной случайной величины более наглядной является не интегральная, а дифференциальная функция распределения или, так называемая, плотность распределения случайной величины:
плотностью распределения 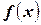 случайной величины
случайной величины  называется производная от её интегральной функции распределения
называется производная от её интегральной функции распределения 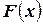 , т.е.
, т.е.
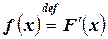 .
.
Свойства дифференциальной функции 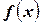 :
:
1. 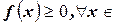 R.
R.
Доказательство этого свойства непосредственно следует из определения. Действительно:
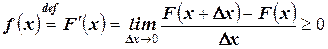
(самостоятельно - объяснить, почему. Рассмотреть различные случаи 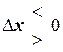 )[6].
)[6].
2. 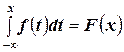 .
.
Доказательство: 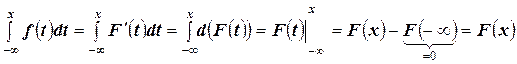 , что и требовалось доказать.
, что и требовалось доказать.
3. 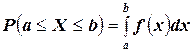 .
.
Доказательство: по четвёртому свойству для интегральной функции 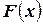 распределения случайной величины можем записать:
распределения случайной величины можем записать: 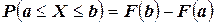 .
.
Но, по рассмотренному выше второму свойству для 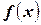 справедливо:
справедливо:
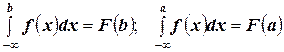 .
.
Тогда
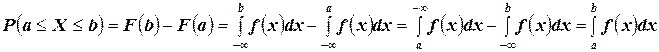 .
.
4. 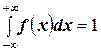 - условие нормировки.
- условие нормировки.
Доказательство. Это свойство, как впрочем и предыдущие, можно доказать различными способами. В частности:
а) 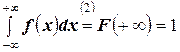 ;
;
б) 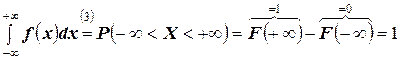 ,
,
что и требовалось показать.
Замечу, что график дифференциальной функции 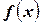 распределения случайной величины лежит выше (или – на) оси
распределения случайной величины лежит выше (или – на) оси 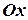 (см. первое свойство) – это, во-первых. Во-вторых, учитывая четвёртое свойство, т.е. условие нормировки, можем также сказать, что площадь области, ограниченной кривой
(см. первое свойство) – это, во-первых. Во-вторых, учитывая четвёртое свойство, т.е. условие нормировки, можем также сказать, что площадь области, ограниченной кривой 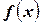 плотности распределения, равна единице.
плотности распределения, равна единице.
ПРИМЕР. Плотность распределения случайной величины  задана формулой
задана формулой 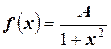 .
.
Требуется:
1. найти величину постоянной  ;
;
2. найти функцию 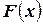 ;
;
3. определить вероятность попадания случайной величины  в интервал
в интервал 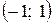 .
.
Решение.
1. величину постоянной  найдём из условия нормировки:
найдём из условия нормировки: 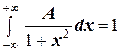 . В нашем случае, получаем
. В нашем случае, получаем
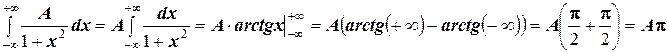 .
.
Следовательно, 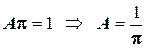 .
.
2. 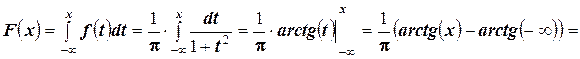
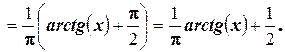
3. 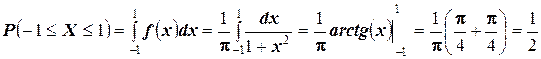 .
.
 2014-02-24
2014-02-24 9583
9583
