Легко указать такие случайные величины, которые имеют одинаковые математические ожидания, но различные возможные значения.
Рассмотрим, например, две дискретные случайные величины X и Y, заданные следующими законами распределения:
| X | -0,01 | 0,01 | Y | -100 | ||
| p | 0,5 | 0,5 | p | 0,5 | 0,5 |
Нетрудно видеть, что M (X)= M (Y)=0. Здесь математические ожидания обеих случайных величин одинаковы, а возможные значения различны, причём Х имеет возможные значения, близкие к математическому ожиданию, а Y – далёкие от своего математического ожидания. Таким образом, зная лишь математическое ожидание случайной величины, ещё нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует.
По этой причине, наряду с математическим ожиданием, вводят и другие числовые характеристики. Так, например, для того, чтобы оценить, как рассеяны возможные значения случайной величины вокруг её математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.
Дисперсией 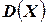 случайной величины называется математическое ожидание квадрата отклонения данной случайной величины от её математического ожидания, т.е.
случайной величины называется математическое ожидание квадрата отклонения данной случайной величины от её математического ожидания, т.е.
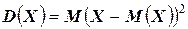 .
.
1). Для дискретной случайной величины: 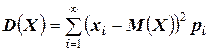
(или 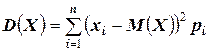 для случайной величины, имеющей конечное число значений);
для случайной величины, имеющей конечное число значений);
2). Для непрерывной случайной величины: 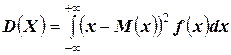
(или 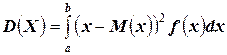 , если значения случайной величины принадлежат промежутку
, если значения случайной величины принадлежат промежутку 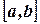 ).
).
Свойства дисперсии 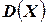 .
.
1. 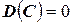 ;
;
2. 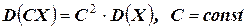 ;
;
3. 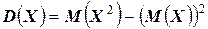 ;
;
4. 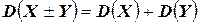 ;
;
5. 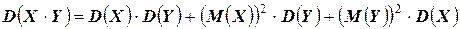 .
.
Доказательства, приведённых выше свойств, вполне очевидны и проводятся по определению. Давайте докажем, например, третье свойство:
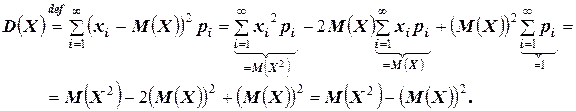
ПРИМЕР. Найти дисперсию 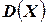 случайной величины
случайной величины  , имеющей следующее распределение
, имеющей следующее распределение

| ||||
| 0,3 | 0,5 | 0,2 | 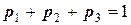
|
РЕШЕНИЕ. Вычислим, прежде всего, математическое ожидание данной случайной величины:
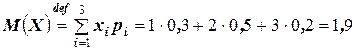 .
.
Тогда, согласно определению дисперсии, получим:
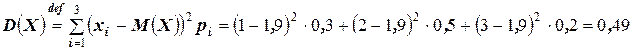 .
.
Удобнее было бы воспользоваться третьим свойством дисперсии. Действительно:
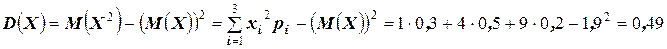 .
.
 2014-02-24
2014-02-24 1157
1157
