Самой простой задачей квантовой механики является задача о движении электрона в кулоновском поле ядра. Это задача об атоме водорода и водорода подобных ионов: однократно ионизированный гелий и однократно ионизированный литий.
Потенциальная энергия взаимодействия электрона с ядром:
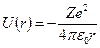 , , | (1) |
где 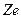 - заряд ядра (для атома водорода
- заряд ядра (для атома водорода 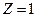 ),
), 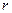 - расстояние между электроном и ядром.
- расстояние между электроном и ядром.
Графически функция 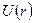 изображена на рис.1. С уменьшением
изображена на рис.1. С уменьшением 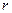 функция
функция 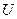 убывает (возрастает по модулю).
убывает (возрастает по модулю).
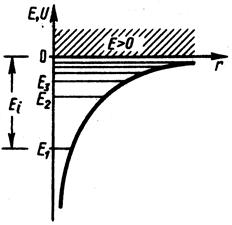 Рис.1. Рис.1. |
Состояние электрон в атоме водорода описывается волновой функцией 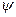 , удовлетворяющей стационарному уравнению Шредингера, учитывающему выражение (1):
, удовлетворяющей стационарному уравнению Шредингера, учитывающему выражение (1):
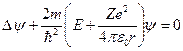 , , | (2) |
где 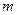 - масса электрона, а
- масса электрона, а 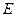 - полная энергия электрона в атоме.
- полная энергия электрона в атоме.
Уравнение (2) имеет решения, удовлетворяющие требования однозначности, конечности и непрерывности волновой функции только при следующих собственных значениях энергии:
 , ( , (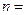 1, 2, 3,…). 1, 2, 3,…). | (3) |
Таким образом, из решения уравнения Шредингера следует, что энергия электрона в атоме квантуется. Формула (3) дает набор дискретных значений энергии, совпадающими со значениями энергии, найденными из спектров. Возможные значения показаны на рис.1. в виде горизонтальных прямых. Самый низкий уровень энергии 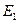 называется основным, все остальные – возбужденными. При
называется основным, все остальные – возбужденными. При 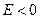 движение электрона является связанным: по мере роста главного квантового числа энергетические уровни располагаются теснее и при
движение электрона является связанным: по мере роста главного квантового числа энергетические уровни располагаются теснее и при 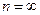
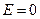 . При
. При 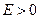 движение электрона является свободным. Область непрерывного спектра
движение электрона является свободным. Область непрерывного спектра 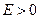 соответствует ионизированному атому. Энергия ионизации атома водорода равна:
соответствует ионизированному атому. Энергия ионизации атома водорода равна:
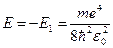 = 13,55 эВ = 13,55 эВ |
 2014-02-09
2014-02-09 1639
1639
