Переходные процессы АД без учёта электромагнитных процессов

Для упрощения расчётов ПП АД в первом приближении пренебрегают электромагнитными ПП.

Рассмотрим процесс запуска АД. Для упрощения примем, что двигатель разгоняется без нагрузки, т.е. 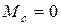, в одну пусковую ступень (прямой пуск).

Уравнение движения:

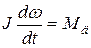
Для АД по формуле Клосса:

,

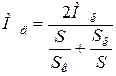т.к. 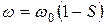, то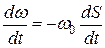

С учётом этого уравнение движения АД примет вид:

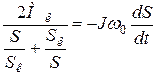
Применяя метод разделения переменных получим:

,

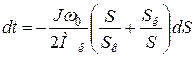где 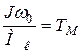- электромеханическая постоянная времени АД.

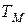- время, в течении которого привод с моментом инерции J разгоняется до синхронной скорости 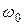под действием момента, равного максимальному М_{к .}

Решая уравнение движения АД получим:

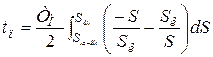
При пуске из неподвижного состояния:

.

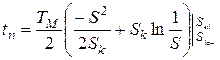Практически, пуск считается закончившимся, когда значение скольжения будет отличатся не более чем на 5% от установившегося значения, т.о. 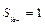и 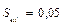. Тогда время пуска при М_с=0:

.

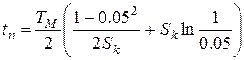Приближенно:

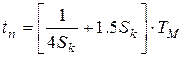
Пользуясь последним выражением, можно определить минимально возможное время пуска АД (рис. 1.4):

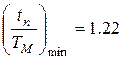при .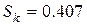

Минимальное время пуска при прочих равных условиях определяется наибольшим эффективным значением динамического момента ЭП.

При .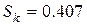

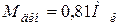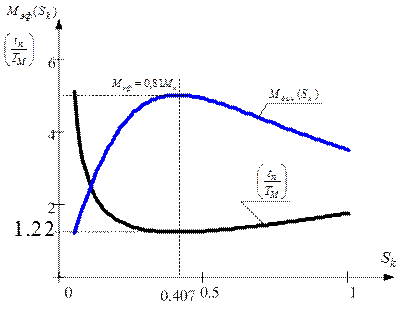
Рис. 1.4. Зависимости относительного времени пуска АД и эффективного электромагнитного момента от критического скольжения