Аппроксимация динамического ряда аналитическими функциями

При аппроксимации динамического ряда известными аналитическими функциями предполагается, что для прогнозирования будет использована функция, у которой форма кривой ближе всего подходит к графическому тренду. Самый простой способ выбора функции – визуальный, на основе графического изображения динамического ряда. Чаще всего для аппроксимации используются:

- линейная функция ;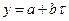

- парабола ;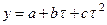

- гипербола ;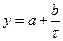

- логарифмическая функция ;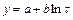

- экспоненциальная функция ;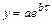

- степенная функция .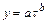

- показательная .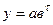

Каждая функция имеет свою сферу применения. Например, линейная функция используется для описания равномерно развивающихся процессов, а гипербола хорошо описывает процессы, для которых характерно насыщение рынка.

Для определения значений эмпирических коэффициентов 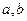и 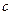обычно используется метод наименьших квадратов. Суть данного метода заключается в определении таких значений эмпирических коэффициентов, которые минимизируют сумму квадратов отклонений расчётных и фактических значений динамического ряда:

,

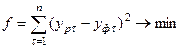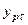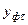где и - расчетные и фактические значения;

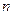- число наблюдений.

Так для линейной функции имеем:

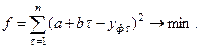
Известно, что функция имеет экстремум, если её производная равна нулю. Дифференцируя функцию по искомым переменным и приравнивая производную нулю, получаем систему линейных уравнений, решая которую найдем неизвестные эмпирические коэффициенты:

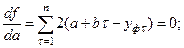или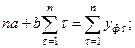

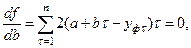
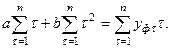
При прогнозировании исследуемого процесса в аналитическую зависимость подставляют вместо параметра 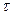порядковый номер следующего прогнозного периода и получают точечное значение прогнозируемого параметра. Так как прогнозируемые процессы носят вероятностный характер, то помимо точечного прогноза, как правило, определяют границы возможного изменения прогнозируемого показателя – доверительные интервалы. Ширину доверительного интервала рассчитывают по формуле:

,

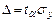где 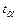- коэффициент доверия по распределению Стьюдента, выбирается в соответствии с принятым уровнем доверительной вероятности (табл. 7);

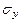- среднее квадратическое отклонение от тренда,

;

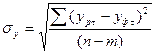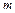- число параметров аналитической зависимости.

Таблица 7

Значения коэффициента доверия по распределению Стьюдента

Уровень доверительной вероятности,	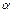0,683	0,95	0,99	0,997
Коэффициент доверия,	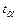	1,96	2,576

Пример. Используя данные задачи из параграфа 2.2.1. составить прогноз объёмов продаж автомобилей на 2006 год используя линейную и параболическую функции.

Решение:

Результаты предварительных расчётов сведём в таблицу 8.