2014-02-24
677
Список используемой литературы
Основные формулы дифференцирования. Таблица производных.
Основные формулы дифференцирования изложены в каждом учебнике курсов «Высшей математики» или «Математики для экономистов», поэтому мы, считаем, что доказательство выводов производных приводить не следует, мы приводим таблицу производных.
Таблица производных
| № | Функция y | Производная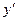 
| № | Функция y | Производная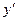
|
| 
| 
| |||
| 
| 
| |||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
| 
| 
| ||
| 
|
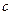
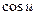
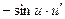
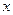
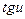
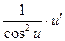
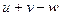
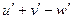
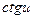
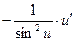
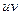
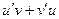
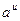
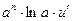
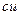
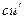
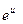
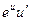
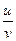
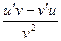
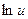
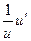
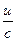
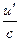
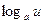
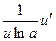
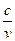
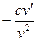
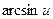
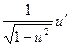
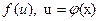
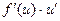
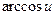
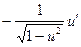
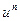
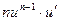
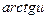
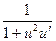
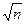
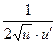
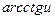
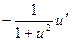
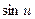
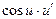
Примеры: Найти производную функций:
а)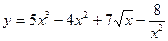 
При решении этого примера воспользуемся формулой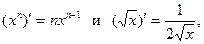 
а также свойством производной, что постоянный множитель можно выносить за знак производной.
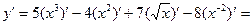
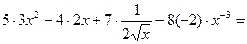
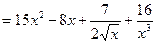
б)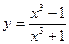 
Данная функция представляет собой дробь, воспользуемся производной частного.
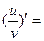
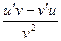
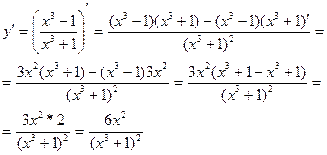
в)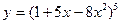 
Это сложная степенная функция. Обозначим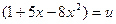 
, тогда 
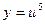. Воспользуемся производной сложной функции.
|
|
|
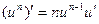
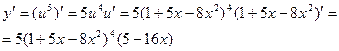
г)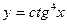 
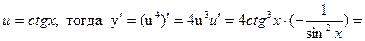
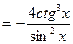
д)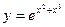 
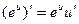
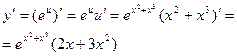
Тесты для самоконтроля знаний.
1.Какая из формул выражает геометрический смысл производной?
а)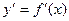 
; б) 
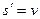; в)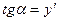 
.
2.Какая из формул выражает механический смысл производной?
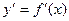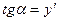а) ; б) ; в)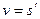 
.
3.Что называется производной от функции y=f(x)
в точке x?
а)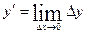 
; б) 
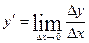; в)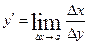 
.
4. По какой формуле вычислите производную функции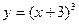 
?
а)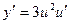 
; б) 
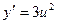; в)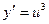 
.
5.Укажите неверную формулу?
а) 
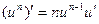; б) 
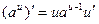; в)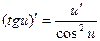 
.
1. Данко, П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов. Ч.1. – М.: ОНИКС. 2003. – 304 с.
2. Данко, П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов. Ч.2. – М.: ОНИКС. 2003 – 415 с
3. Ермаков, В.И. Сборник задач по высшей математике. Учебное пособие. –М.: ИНФРА-М, 2006. – 575 с
4. Ермаков, В.И. Общий курс высшей математики. Учебник. –М.: ИНФРА-М, 2003. – 656 с.
5. Колесников, А.Н. Краткий курс математики для экономистов: Учебное пособие. М.: ИНФРА-М.,2001, - 208 с.
Тема «Производная»
Цель: дать понятие дифференциала функции, выявить его свойства и показать применение дифференциала в приближенных вычислениях.
Ключевые слова: дифференциал, бесконечно малая величина.
Вопросы:
1. Понятие дифференциала функции. Геометрический смысл дифференциала.
2. Свойства дифференциала. Инвариантность формы дифференциала.
3. Применение дифференциала в приближенных вычислениях.
