Понятие дифференциала функции.
Пусть фукция y=f(x) дифференцируема при некотором значении х 0. Следовательно, в точке х существует конечная производная 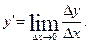 По определению предела
По определению предела 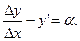
Эта величина называется бесконечно малой при 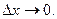 Найдем
Найдем 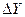 :
: 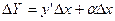 .
.
y’ от 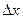 не зависит, она остается постоянной при
не зависит, она остается постоянной при 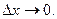
Если 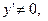 то
то 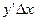 - является бесконечно малой величиной того же порядка малости, что и
- является бесконечно малой величиной того же порядка малости, что и 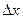 .
.
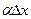 - бесконечно малая более высокого порядка малости, чем первое слагаемое. Поэтому
- бесконечно малая более высокого порядка малости, чем первое слагаемое. Поэтому 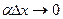 , величину
, величину 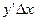 (
(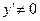 ) называют главной, линейной относительной
) называют главной, линейной относительной 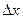 частью приращения функции; чем меньше
частью приращения функции; чем меньше 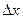 , тем большую долю приращения составляет это выражение.
, тем большую долю приращения составляет это выражение.
Поэтому при малых значениях 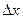 приращение функции можно заменить
приращение функции можно заменить 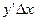 , т.е.
, т.е.
и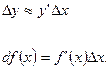
Эту главную часть приращения функции называют дифференциалом функции в точке х и обозначают dy или df(x), следовательно 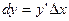 или
или 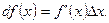
Дифференциал равен произведению ее производной на приращение независимой переменной.
f(x)=x, dx=x’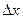 =
=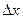 ,
, 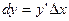 ,
, 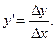
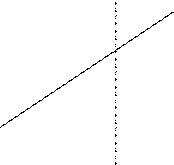
Рассмотрим график дифференцируемой функции y=f(x). Пусть М и М’ – точки графика, имеющие соответственно координаты М(х; у) и 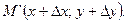
 y
y

 M1
M1
 |
∆y

 N dy
N dy
|


 М Р
М Р
 x x+∆x
x x+∆x  x
x
MN- касательная к графику y=f(x).
При изменении аргумента от x до 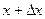 ордината точки M графика функции получит приращение
ордината точки M графика функции получит приращение 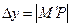 , а ордината касательной -приращение
, а ордината касательной -приращение 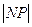 ;
;
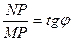 ,
, 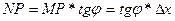 ,
,
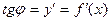
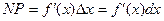
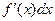 - дифференциал функции.
- дифференциал функции.
Таким образом, дифференциал функции y=f(x) равен приращению ординаты касательной, проведенной к графику этой функции в точке (x;y) при изменении x на величину 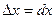 . В этом и состоит геометрический смысл дифференциала.
. В этом и состоит геометрический смысл дифференциала. 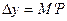 ,
, 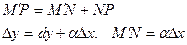 .
.
 2014-02-24
2014-02-24 847
847








