Формы дифференциала

Свойства дифференциала. Инвариантность

Дифференциал обладает свойствами, аналогичными свойствам производной. Запишем их:

1.

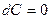
2.

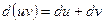
3.

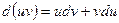
4.

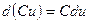
5.

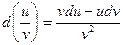
Эти формулы получаются из формул производных умножением обеих частей на 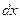.Рассмотрим свойство, которым обладает дифференциал функции, но не обладает ее производная. Если дана функция 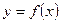, то ее дифференциал равен 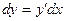(1)

Рассмотрим функцию 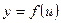, где аргумент 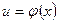сам является функцией от х, т.е. рассмотрим сложную функцию 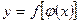. Если функци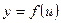и и 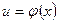дифференцируемые функции от своих аргументов, то производная сложной функции равна 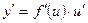. Тогда дифференциал функции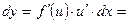 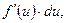так как по формуле (1) 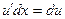. Итак 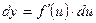(2)

Равенство (2) означает, что формула дифференциала не изменяется, если вместо функции независимой переменной х рассматривать функцию от зависимой переменной u. Это свойство дифференциала получило название инвариантности (т.е. неизменности) формы дифференциала.