а) Формула интегрирование по частям для вычисления определенного интеграла имеет вид: 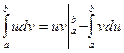 (4)
(4)
Пример. Вычислить 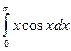
Решение.
Положим, что x=u, cosxdx=dv, то dx=du, v=sinx
Применяя формулу интегрирования по частям, найдем
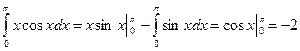
так как 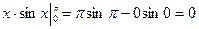
б) Пусть дан определенный интеграл 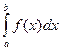 и по каким-то соображениям нам желательно ввести новую переменную t, связанную с прежней x соотношением
и по каким-то соображениям нам желательно ввести новую переменную t, связанную с прежней x соотношением
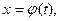 где
где 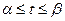
При изменении t от α до β переменная x меняется от a до b,
т.е. 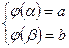 (5)
(5)
Тогда справедлива формула:
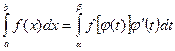 (6)
(6)
Эта формула перехода к новой переменной под знаком определенного интеграла.
Замечание. При вычислении определенного интеграла с помощью замены переменной нет необходимости возвращаться к прежней переменной.
Пример. Вычислить определенный интеграл
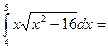
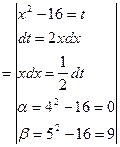
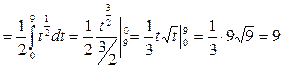
 2014-02-24
2014-02-24 579
579








