Понятие о приближенном вычислении определенных интегралов. Формула трапеций

Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур.

1.Определенный интеграл от непрерывной неотрицательной функции f(x) при a ≤ b равен площади соответствующей криволинейной трапеции, т.е.

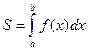(7) или 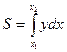(7`) – площадь криволинейной трапеции прилежащей к оси OX

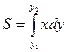, где (8) – площадь криволинейной трапеции, прилежащей к оси OY.

2.Если 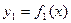, а 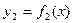на [a,b], то площадь плоской фигуры, заключенной между ними равна:

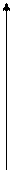
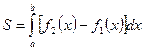
3.Если кривая, заданная уравнением y=f(x) на отрезке [a,b], пересекает ось OX в точках 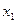и 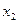и расположена между этими точками под осью OX, то вся площадь фигуры выразится так:

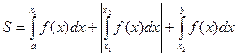
Пример. Вычислить площадь фигуры S, ограниченной кривыми y= -x² и y=e^x, осью ординат и прямой x=1

Решение.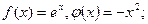

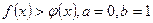
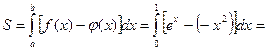
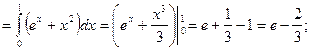
Ответ: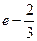

Определенный интеграл 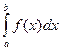от заданной непрерывной функции y=f(x) на отрезке [a,b] вычисляется не всегда точно. Пользуясь его геометрическим смыслом можно дать ряд приближенных формул, с помощью которых этот интеграл находится с любой степенью точности. Рассмотрим из них, так называемую формулу трапеций

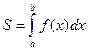- площадь криволинейной трапеции

Разобьем отрезок [a,b] на n равных частей,

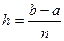- шаг разбиения.

Пусть 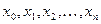- абсциссы точек деления

и 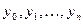- соответствующие ординаты кривой.

В результате построения криволинейная трапеция разбилась на ряд вертикальных полосок одной и той же ширины h, каждую из них приближенно примем за трапецию.

Суммируя площади имеем:

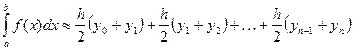
или

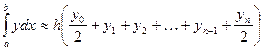- формула трапеций.