Интегрирование простейших дробей типов
а) 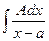 и б)
и б) 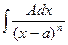 ;
;
а) 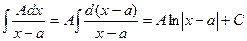 ,
,
б)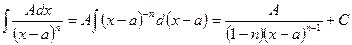
Пусть знаменатель Q(x) рациональной дроби 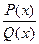
разлагается на множители следующим образом
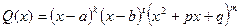 , где квадратный трехчлен не имеет действительных корней. Тогда имеет место следующая теорема:
, где квадратный трехчлен не имеет действительных корней. Тогда имеет место следующая теорема:
Правильную рациональную дробь 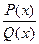 ,
,
где 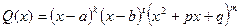 ,
,
можно единственным образом разложить в сумму простейших дробей:
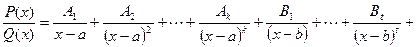 +
+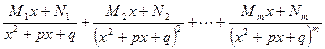 ,
,
где 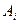 ,
,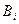 ,
,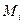 ,
, 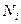 - действительные числа (i=1,2,…)
- действительные числа (i=1,2,…)
Одним из наиболее простых методов определения коэффициентов в разложении правильной дроби на простейшие является метод неопределенных коэффициентов.
Пример.
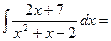
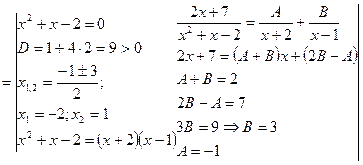 =
=
=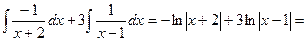
=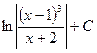
Тестовые вопросы для самоконтроля знаний.
1. Неопределенный интеграл имеет вид:
A) 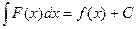 , B)
, B) 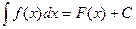 ,
,
C) 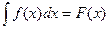 , D)
, D) 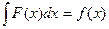 ,
,
E) 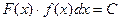
2.Какая из следующих формул правильная?
A) 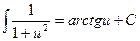 , B)
, B)  ,
,
C) 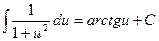 , D)
, D) 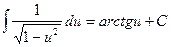 ,
,
E) 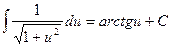
3.Составить уравнение кривой, если угловой коэффициент касательной в каждой ее точке (x,y) равен –3x
A) 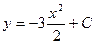 , B)
, B) 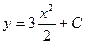 , C)
, C) 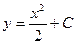 ,
,
D) 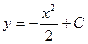 , E)
, E) 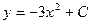
4. Формула интегрирования по частям имеет следующий вид:
A) 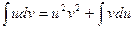 , В)
, В) 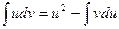 ,
,
C) 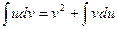 , D)
, D) 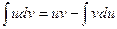 ,
,
E) 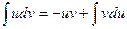
5. Найти интеграл 
A) 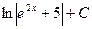 , B)
, B) 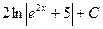 , C)
, C) 
D) 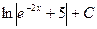 , E)
, E) 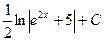
 2014-02-24
2014-02-24 424
424








