Теорема: пусть дан положительный ряд
U1+U2+U3+…+Un+… (1)
с убывающими членами 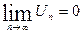 .
.
а f(x), определенная в промежутке [1,+
f(x), определенная в промежутке [1,+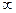 } монотонно убывает в нем и при х=n принимает значения
} монотонно убывает в нем и при х=n принимает значения
f(n)=Un,
тогда данный ряд сходится, если сходится несобственный интеграл
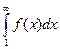
и расходится в противном случае.
Теорему принимаем без доказательства.
Пример 5: исследовать по интегральному признаку ряд
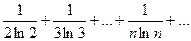
Решение: f(n)=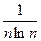
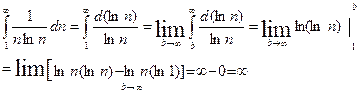
несобственный интеграл не существует, следовательно ряд расходится.
Замечание: Интегральный признак Коши позволяет сделать заключение о характере ряда в тех случаях, когда признаки Даламбера и Коши оказываются бессильными (т.е. тогда, когда получается,что 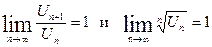 ). Поэтому интегральный признак Коши следует считать сильнее этих признаков. Тем не менее на практике применение интегрального признака часто вызывает затруднения, связанные с вычислением несобственного интеграла
). Поэтому интегральный признак Коши следует считать сильнее этих признаков. Тем не менее на практике применение интегрального признака часто вызывает затруднения, связанные с вычислением несобственного интеграла 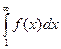 .
.
 2014-02-24
2014-02-24 1556
1556