Описание процесса теплообмена в КС двигателя с плоским поршнем и плоской головкой

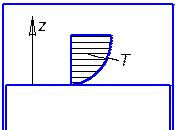
Рассмотрим вопросы моделирования условий теплообмена для поверхностей поршня и головки цилиндров. Так как касательной составляющей скорости к этим поверхностям нет, нет и условий для конвекции. Следовательно, дело будем иметь с теплопроводностью через некий слой газа толщиной d_т. Такой характер теплообмена принято называть кондуктивным. Изначально будем считать, что задача трех-мерная. При поставленных условиях распределение температур в пограничном слое толщиной d_т описышется уравнением Фурье:

.

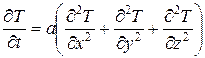(90)

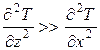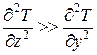В данном случае и , поскольку порядок d_т, много меньше, чем линейный размер КС, поэтому задачу теплопроводности можно считать одномерной:

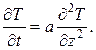
(91)

Произведем оценку составляющих в данном выражении, составив отношение правой части к левой:

.

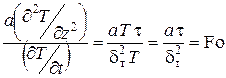Полученное соотношение есть число Фурье, являющееся мерой тепловой нестационарноти процесса. Произведем его численную оценку, использовав следующие соотношения:

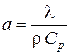– коэффициент температуропроводности, где C_p – удельная теплоемкость заряда при постоянном давлении;

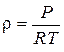– плотность заряда в цилиндре, R – газовая постоянная;

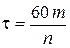– характерное время протекания цикла, m – к-т тактности;

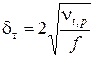– толщина пристенного слоя газа (по Линь-цзя-Цзяо);

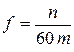– частота повторения циклов.

После подстановки указанных выражений и некоторых приведений получим:

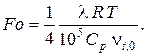
(92)

Оценим порядок полученного выражения:

.

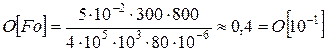Поскольку число Фурье весьма мало, следует сделать неутешительный вывод: задачу следует рассматривать как нестационарную. Здесь возможны два варианта. Первый – решить задачу как квазистационарную, а нестационарность процесса теплообмена учесть поправкой вида (52). Второй – решать задачу в прямой нестационарной постановке.

Для начала, решим задачу определения поля температур в пограничном слое как квазистационарную, положив 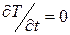, тогда:

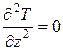, или в полных производных: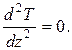

Последнее уравнение можно дважды проинтегрировать:

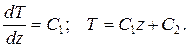
Используем граничные условия:

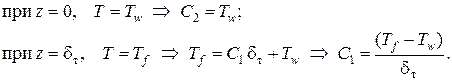
Окончательное выражение для распределения температур в пограничном слое получим в виде:

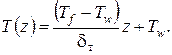
(93)

Получим граничные условия 3-го рода, для чего воспользуемся гипотезой Фурье о тепловом потоке:

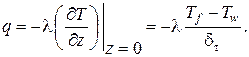
Согласно формуле Ньютона:

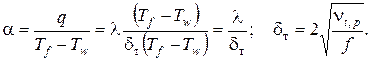
Окончательно:

.

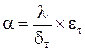(94)

Таким образом, получили достаточно простое выражение для коэффициента теплоотдачи. Поправка e_t должна учесть тепловую нестационарность процесса (см. § 2.6.3).

Рассмотрим ту же задачу в нестационарной постановке:

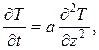
где T = T (t, z) – искомая функция распределения температур в ПС.

Поставим граничные условия:

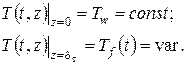
Введем приращение температуры: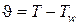, тогда 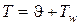и

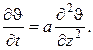
(95)

Граничные условия для последнего выражения запишутся в виде:

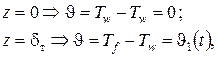
(96)

где J₁(t) – известное значение мгновенного температурного напора.

Введем новую поперечную координату:

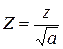, тогда ,

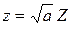и сделаем ее подстановку в (95), тогда:

.

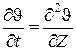(97)

Граничные условия для (97) перепишем в виде:

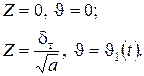
(98)

Уравнение (98) решается путем введения двух новых функций – координаты Z и времени t с последующим разделением переменных и введением собственных чисел решения. Распределение температур в ПС окончательно имеет вид:

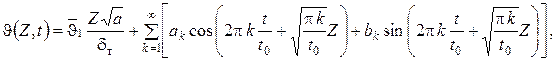
(99)

где 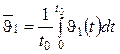– средний за цикл температурный напор; t ₀ – период цикла; t – текущее время от начала цикла; a_k, b_k – коэффициенты разложения, имеющие размерность температуры, которые можно получить путем согласования общего решения (99) с граничными условиями (98). Причем a_k, b_k являются функциями комплекса .

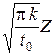Определим граничные условия 3-го рода (получим коэффициент теплоотдачи), приравняв выражения Фурье и Ньютона:

.

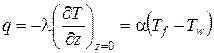Перейдем к введенным ранее переменным, и в первую очередь к приращению температуры J:

.

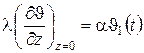Выразим отсюда коэффициент теплоотдачи:

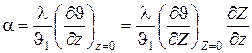, и поскольку ,

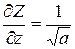получим:

.

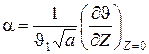(100)

Далее возьмем производную по Z от общего решения (99) для распределения температур в пограничном слое и положим Z = 0 в полученном выражении:

.

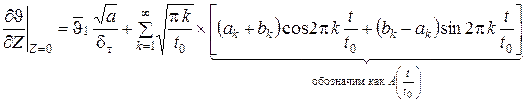(101)

Подставив (101) в (100) получим:

.

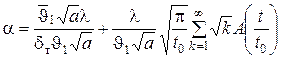(102)

Поскольку 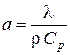, окончательно получаем:

,

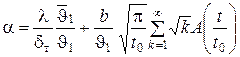(103)

где 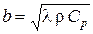– коэффициент проникновения теплоты.

Таким образом, коэффициент теплоотдачи складывается из двух частей:

,

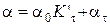где a₀ – отражает стационарную составляющую интенсивности теплоотдачи, а a_t – пульсационную, зависящую от текущего времени.

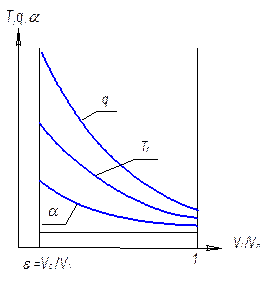На рис. ХХ показано изменение температуры газа, коэффициента тепло-отдачи и плотности теплового потока, впервые полученные Никаджаном и Грейфом [2] для процесса сжатия в поршневом компрессоре.

Полученный в данном параграфе коэффициент теплоотдачи можно рассматривать как нижний предел интенсивности теплоотдачи в камере сгорания при отсутствии движения заряда.