Рассмотрим движение рабочего тела в профилированной камере сгорания (фигурный профиль имеет поршень). Считаем, что головка цилиндров плоская, а потому движение заряда будет инициироваться именно поршнем. Рассмотрим ядро потока с принятыми ранее допущениями о квазиравновесности и квазистационарности протекающего процесса.
Будем рассматривать процессы при постоянной массе (или при закрытых органах газораспределения). Будем также считать, что в начальный момент сжатия заряд движения не имеет. Примем, что профиль поршня симметричен относительно оси цилиндра (рис. ХХ).
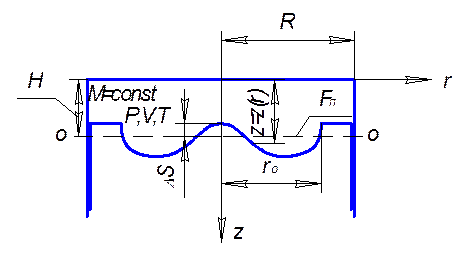
Рис. ХХ. Расчетная схема открытой КС дизеля
Плоскость О-О выберем из соображений, чтобы объем цилиндра, образовавшегося выше этой плоскости был бы равен истинному объему камеры сжатия.
Введем обозначения: F п – площадь проекции поршня; H – текущее расстояние от головки цилиндра до плоскости О-О; Z (r) – текущее расстояние от поверхности головки цилиндра до точек на поверхности поршня; r 0 – радиус профилированной части поршня (горловины): D S – расстояние от плоскости О-О до профиля поршня в его центральной части.
В любой момент времени масса рабочего тела M = V r. Возьмем логарифмическую производную от этого выражения:
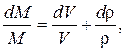
| (104) |
и поскольку 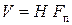 , а M = const, то
, а M = const, то
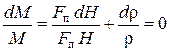 .
.
Сократив F п и разделив обе части уравнения на dt, получим:
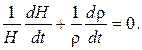
| (105) |
Поскольку 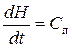 , окончательно получим:
, окончательно получим:
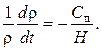
| (106) |
Для описания движения газа в цилиндре воспользуемся уравнением сплошности несжимаемой среды в нестационарной постановке:
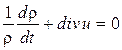 . .
| (107) |
Сравнивая выражения (106) и (107), получим:
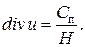
| (108) |
Это и есть основное уравнение, описывающее движение заряда в цилиндре двигателя, причем
для плоской задачи: 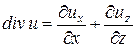 ,
,
а для осесимметричной: 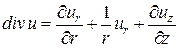 .
.
При записи (108) следует отметить следующее. Во-первых, уравнение сплошности не является основным уравнением движения (в частности Эйлера) для невязкого газа. Однако такой подход нередко применяют для получения относительно простых решений применительно к “потенциальных” течениям газа, характеризующегося развитой турбулентностью. Во-вторых, уравнение (108) отражает прямой нестационарный подход к решению газодинамической задачи для ядра потока.
Далее будем рассматривать осесимметричный случай. Перепишем уравнение (108):
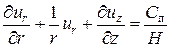 . .
| (109) |
Введем потенциал скорости 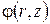 так, что
так, что
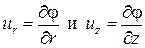 .
.
Подставив потенциалы скорости в исходное уравнение, получим:
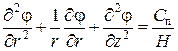 . .
| (110) |
Граничные условия, в соответствии с условиями непроницаемости стенок имеем следующие:
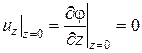 и и 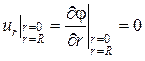 . .
| (111) |
Уравнение (110) – линейное неоднородное в частных производных второго порядка. Общее решение будем искать в виде суммы однородного уравнения с нулевой правой частью j0 и решения, обусловленного видом правой части – dj, т.е.:
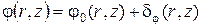 . .
| (112) |
Выразим профиль поршня некоторой функцией:
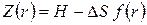 , ,
| (113) |
где f (r) – функция профиля поршня.
Запишем условие равенства объемов над плоскостью О-О и истинного объема цилиндра, исходя из (113):
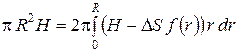 . .
| (114) |
После выноса постоянной из-под знака интеграла, имеем:
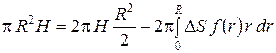 .
.
После очевидных сокращений получаем:
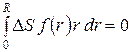 . .
| (115) |
Выражение (115) представляет собой условие нормировки объема камеры сгорания (рис. ХХ).
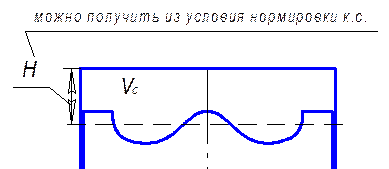
Рис. ХХ. К определению условия нормировки КС
Введем относительный текущий радиус 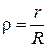 и функцию профиля поршня f (r), которую аппроксимируем полиномом n -ой степени:
и функцию профиля поршня f (r), которую аппроксимируем полиномом n -ой степени:
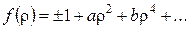 . .
| (116) |
В этом выражении положим r = 1, что соответствует r = R, тогда
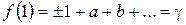
| (117) |
– характеристика профиля поршня, которая характеризует степень кривизны его поверхности.
Сделаем следующий ход: домножим (110) на z, тогда получим:
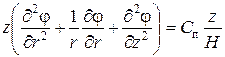 . .
| (118) |
Следует заметить, что правая часть полученного уравнения в точности равна осевой проекции вектора скорости для плоскопараллельной камеры сгорания и представляет собой линейное распределение скоростей вдоль поверхности гильзы цилиндра.
Далее будем искать решение для относительно неглубоких камер сгорания, тогда с некоторой степенью точности посчитаем, что профиль скорости вдоль оси z такой же, как для плоскопараллельной камеры сгорания. То есть, будем считать, что составляющую скорости uz (r, z) мы нашли и она, в предположении малой глубины КС, равна:
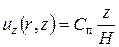 . .
| (119) |
Остается найти вторую составляющую скорости ur (r, z).
Установим связь общего решения (112) с условием нормировки (115) при условии z = Z – на поверхности поршня. Поскольку 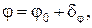 составляющая скорости uz может быть представлена как
составляющая скорости uz может быть представлена как
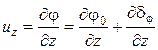 ; ;
| (120) |
с другой стороны на поверхности поршня:
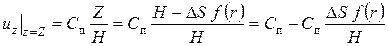 . .
| (121) |
Очевидно, приняв (119), мы приняли, что вид правой части исходного уравнения определяет “переносную” составляющую движения заряда, связанную с возвратно-поступательным движением поршня со скоростью C п. Тогда можно сказать, что 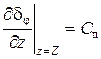 , поскольку часть общего решения dj обусловлена видом правой части (110).
, поскольку часть общего решения dj обусловлена видом правой части (110).
Другая часть решения 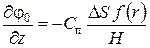 – по всей видимости, обусловлена “вытеснительным” действием профиля поршня.
– по всей видимости, обусловлена “вытеснительным” действием профиля поршня.
Запишем аналогичное выражение для составляющей скорости ur:
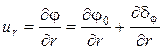 , ,
| (122) |
причем очевидно, что 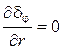 , поскольку переносного движения вдоль радиуса цилиндра нет. Теперь для нахождения скорости ur от уравнения (110) остается только выражение для составляющей j0 для нулевой правой части (поскольку последняя обуловила решение для uz):
, поскольку переносного движения вдоль радиуса цилиндра нет. Теперь для нахождения скорости ur от уравнения (110) остается только выражение для составляющей j0 для нулевой правой части (поскольку последняя обуловила решение для uz):
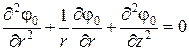 . .
| (123) |
Граничные условия для уравнения (123):
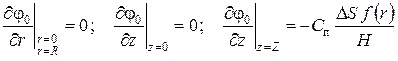 . .
| (124) |
Уравнение (123) с граничными условиями (124) решается путем введения двух функций, одна из которых является функцией r, другая – функцией z, разделением переменных и введением собственных чисел решения Pk 2. В результате чего определяется функция j0(r, z), а радиальная составляющая скорости ur (r, z)определится из выражения:
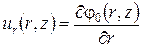 . .
| (125) |
В итоге, выражение для ur (r, z)выглядит так:
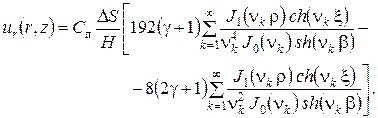
| (126) |
Здесь: 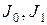 – функции Бесселя 1-го рода 0-го и 1-го порядков;
– функции Бесселя 1-го рода 0-го и 1-го порядков;
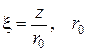 – максимальный радиус горловины камеры в поршне;
– максимальный радиус горловины камеры в поршне;
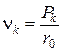 – относительные собственные числа решения;
– относительные собственные числа решения; 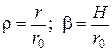 ,
,
H – расстояние от срединной плоскости поршня до крышки цилиндра.
Таким образом, газодинамическая задача для ядра потока решена – получено поле скоростей в КС в виде составляющих ur (r, z) и uz (r, z). Однако для расчета теплоотдачи необходимо знать касательные скорости обтекания отдельных поверхностей камеры сгорания. Определим их.
Для поверхности головки z = 0, тогда:
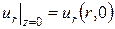 , а , а 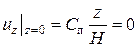 . .
| (127) |
Для поверхности втулки r = R, тогда:
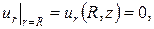 а а 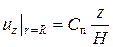 . .
| (128) |
Для поверхности поршня z = Z (r), тогда:
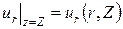 , а , а 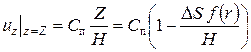 . .
| (129) |
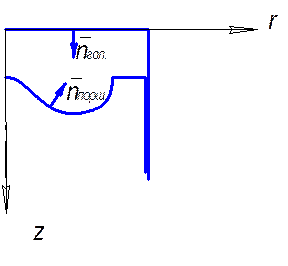
Таким образом, определили проекции вектора скорости на интересующих нас стенках. Для определения касательных скоростей воспользуемся направляющими косинусами к поверхностям КС (рис. ХХ).
Для головки: 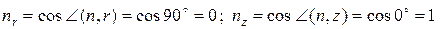 , тогда поскольку uz = 0,
, тогда поскольку uz = 0, 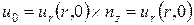 .
.
 Для втулки, поскольку ur = 0,
Для втулки, поскольку ur = 0, 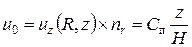 , т.к. nr = 1.
, т.к. nr = 1.
Для поршня:
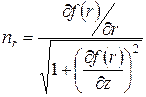 ;
; 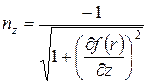 .
.
Тогда:
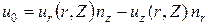 , или:
, или:
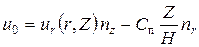 . .
| (130) |
Рассмотрим теперь течение газа в камере сгорания (рис. ХХ).
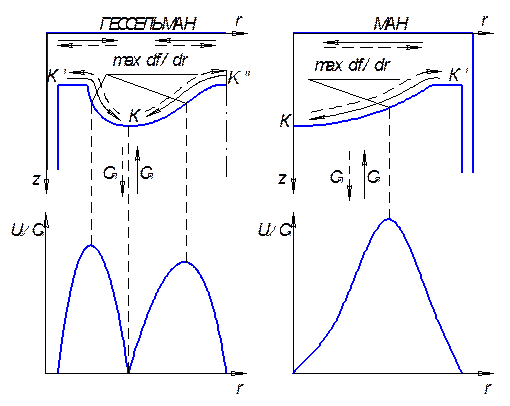
Рис. ХХ. Картина обтекания поверхностей открытых КС дизелей.
Здесь: К – точка, где касательная скорость на стенке равна нулю
Выводы:
1) Полученное решение справедливо для относительно неглубоких камер сгорания открытого типа. Предельный случай – ЯМЗ, КамАЗ.
2) В отличие от плоскопараллельной камеры сгорания имется интенсивное обтекание поверхностей головки и поршня, инициированное профилем поршня, следовательно для них тип теплообмена будет определенно конвективным, а значит и интенсивность теплоотдачи здесь будет явно выше, чем в плоскопараллельной камере сгорания.
В общем случае, чем глубже камера сгорания, тем интенсивнее движение заряда в ней, а следовательно, выше средний коэффициент теплоотдачи и уровень теплонапряженности деталей, ограничивающих камеру сгорания.
3) Касательная скорость обтекания поверхностей КС u 0 = var, следовательно движение газа вблизи стенки будет градиентным.
 2014-02-24
2014-02-24 823
823








