Постоянная Планка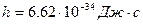 .
.
Масса электрона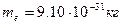 .
.
Заряд электрона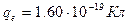 .
.
Число Авогадро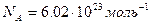 .
.
Постоянная Больцмана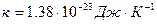 .
.
Универсальная газовая постоянная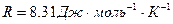 .
.
Объем моля идеального газа при нормальных условиях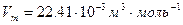 .
.
Постоянная Лошмидта (число молекул в одном кубическом метре вещества, находящегося в состоянии идеального газа при нормальных условиях) 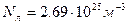 .
.
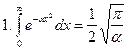
(интеграл Пуассона)
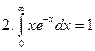
Найти нормировочную константу А для каждого случая. Построить соответствующие графики плотности вероятности.
1.4. Проверить выполнение условия нормировки вероятности в задаче 1.1.
1.5. Представим себе тонкую медную проволоку, натянутую вдоль оси Х. Несколько атомов меди, расположенных вблизи х =0, сделали "мечеными" (радиоактивными). При увеличении температуры нити подвижность атомов возрастает. При этом каждый атом может перескочить на соседнее место в кристаллической решетке либо направо, либо налево. Параметр решетки равен l.
Предположим, что в момент времени t =0 температура нити быстро возрастает до некоторого большого значения и в дальнейшем остается неизменной, т.е. до момента t =0 атомы "не прыгали", а покоились в узлах решетки, в том числе и "меченые" атомы в окрестности x =0.
Вероятность того, что радиоактивный атом будет обнаружен по истечении времени t при условии, что t>>t (t - время нахождения атома в узлах решетки), в интервале [x, x+dx] определяется плотностью вероятности f(x), dP(x) = f(x)dx. Изобразить на графике примерный ход плотности вероятности в зависимости от x, исходя из соображений симметрии и условия нормировки, для следующих трех случаев:
а) вскоре после t =0,
б) по прошествии относительно большого времени t,
в) по прошествии очень большого времени t.
 2014-02-24
2014-02-24 362
362








