О т в е т ы
5.1. 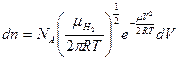 , подставив данные
, подставив данные
 (постоянная Авогадро),
(постоянная Авогадро),  , T =300K, V =500 м/с,
, T =300K, V =500 м/с, 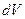 =2 м/с, R =8,31
=2 м/с, R =8,31  , получаем
, получаем 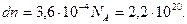
5.2. Значения всех величин равны нулю.
5.3. 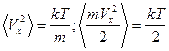 .
.
5.4. 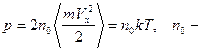 концентрация идеального газа.
концентрация идеального газа.
5.5. a) 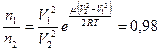 , б)
, б) 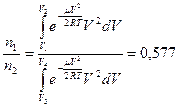 .
.
5.6. 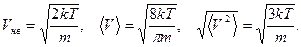
5.7. 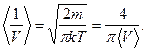
5.8. 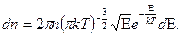
5.9. 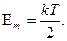
5.10. 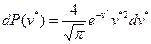
5.11. 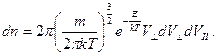
5.12. 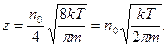
5.13. Для изотропного распределения 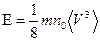 .
.
Для распределения Максвелла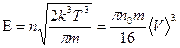 .
.
Если идеальный газ находится в силовом поле, то его состояние может быть нестационарным, неравновесным. Тогда распределение Гиббса для него неприменимо. Только некоторые потенциальные поля приводят молекулярную систему к тепловому равновесию и стационарному распределению частиц в пространстве. Такими полями являются однородное гравитационное поле, поле центробежных сил и электростатическое поле. В этих трех случаях распределение Гиббса применимо. Т.к. потенциальная энергия частицы не зависит от ее скорости, а кинетическая энергия не зависит от координаты частицы, то можно рассматривать распределение по скоростям и по координатам отдельно. Распределение частиц по скоростям описывается распределением Максвелла, а пространственное распределение частиц описывается распределением Больцмана. В общем случае, если потенциальная энергия частицы зависит от трех координат -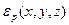 , то распределение Больцмана имеет следующий вид:
, то распределение Больцмана имеет следующий вид:
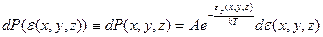 (7.1).
(7.1).
В однородном гравитационном поле(g=const) потенциальная энергия частицы равна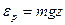 и распределение Больцмана записывается:
и распределение Больцмана записывается:
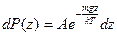 . (7.2)
. (7.2)
На основании того, что 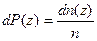 , из (7.2) получается выражение для пространственной концентрации частиц
, из (7.2) получается выражение для пространственной концентрации частиц 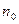 как функции от высоты z:
как функции от высоты z:
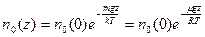 , (7.3)
, (7.3)
где 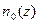 – концентрация частиц на высоте z,
– концентрация частиц на высоте z, 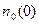 -концентрация на высоте, где потенциальная энергия равна нулю,
-концентрация на высоте, где потенциальная энергия равна нулю, 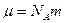 – молярная масса газа, R=8,314 Дж/(моль×К) (универсальная газовая постоянная). Выражение для
– молярная масса газа, R=8,314 Дж/(моль×К) (универсальная газовая постоянная). Выражение для 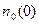 может быть получено из условия сохранения количества частиц в газовом столбе высотой Н и площадью сечения S =1
может быть получено из условия сохранения количества частиц в газовом столбе высотой Н и площадью сечения S =1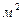 :
:
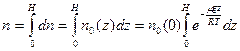 ,
,
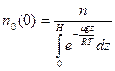 . (7.4)
. (7.4)
В поле центробежных сил, например, во вращающейся с угловой скоростью 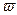 центрифуге,
центрифуге, 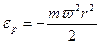 – потенциальная энергия молекулы зависит от ее удаленности r от оси вращения. В этом случае пространственная концентрация определяется следующим образом:
– потенциальная энергия молекулы зависит от ее удаленности r от оси вращения. В этом случае пространственная концентрация определяется следующим образом:
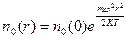 , (7.5)
, (7.5)
где 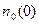 – концентрация частиц на оси вращающегося цилиндра. Значение этой величины можно получить из условия сохранения полного числа частиц в объеме
– концентрация частиц на оси вращающегося цилиндра. Значение этой величины можно получить из условия сохранения полного числа частиц в объеме 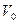 цилиндра радиуса R и высоты H.
цилиндра радиуса R и высоты H.
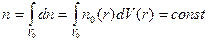 . (7.6)
. (7.6)
Так как 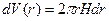 , то выражение (7.6) примет вид
, то выражение (7.6) примет вид
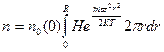 , (7.7)
, (7.7)
отсюда получается выражение для 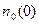 :
:
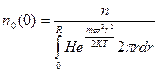 . (7.8)
. (7.8)
 2014-02-24
2014-02-24 457
457








