2014-02-24
566
а) Линеаризация относительно положения равновесия.
Динамический режим работы системы задан уравнениями (2.4) или (2.5). Пусть для системы существует стационарный режим, определяющий её положение равновесия, т.е.
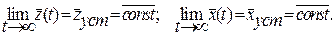
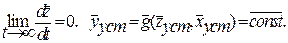(2.8)
Таким образом, в положении равновесия вектора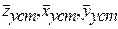 
- постоянные. Если отклонения 
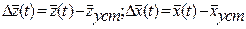достаточно малы, то линеаризация уравнений (2.4) или (2.5) приводит к уравнениям вида
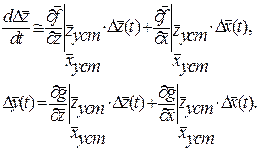
Частные производные вектор-функци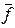й 
и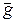 
по составляющим векторов 
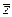и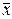 
образуют матрицы A, B, C, D, все элементы которых постоянны.
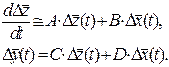(2.9)
b) Линеаризация относительно опорного динамического режима.
Пусть задан некоторый динамический режим работы системы (опорный режим), т.е. заданы вектор-функции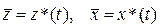 
, на отрезке времени 
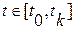. Если отклонения 
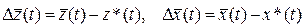невелики, то линеаризованые уравнения совпадают с уравнениями (2.9), но матрицы коэффициентов в них 
, 
, 
, 
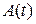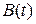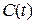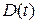- являются функциями времени.
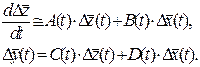(2.10)
