Передаточной функцией W(s) комплексной переменной s называется отношение изображения выходной величины 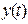 к изображению входного воздействия
к изображению входного воздействия 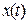 при нулевых начальных условиях. Нулевые начальные условия для линейных непрерывных систем всегда предполагаются. (Этот вопрос будет рассмотрен ниже при описании временных характеристик). Таким образом,
при нулевых начальных условиях. Нулевые начальные условия для линейных непрерывных систем всегда предполагаются. (Этот вопрос будет рассмотрен ниже при описании временных характеристик). Таким образом,
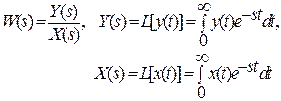 (2.13)
(2.13)
где 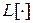 – оператор прямого преобразования Лапласа,
– оператор прямого преобразования Лапласа, 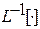 - оператор обратного преобразования Лапласа.
- оператор обратного преобразования Лапласа.
Чтобы получить передаточную функцию системы, заданной уравнением (2.11), необходимо к обеим частям этого уравнения применить преобразование Лапласа. Тогда передаточная функция W (s) представляется в виде отношения двух полиномов комплексной переменно s.
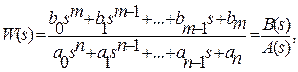 (2.14)
(2.14)
где 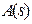 и
и 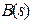 – обозначение полиномов.
– обозначение полиномов.
Приравнивая нулю, полином знаменателя, называемый характеристическим, формируется характеристическое уравнение
 . (2.15)
. (2.15)
Решением этого алгебраического уравнения являются значения n корней характеристического уравнения или полюсов передаточной функции 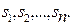
Аналогично, приравнивая нулю полином числителя 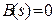 получаем в качестве решения нули передаточной функции
получаем в качестве решения нули передаточной функции 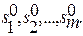 Тогда, используя теорему Виета, передаточная функция представляется в виде
Тогда, используя теорему Виета, передаточная функция представляется в виде
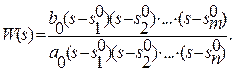
В зависимости от того, являются ли полюса 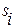 или нули
или нули  вещественными или комплексно-сопряженными, передаточная функция представляется в виде произведения передаточных функций определенного набора типовых звеньев. Например,
вещественными или комплексно-сопряженными, передаточная функция представляется в виде произведения передаточных функций определенного набора типовых звеньев. Например,
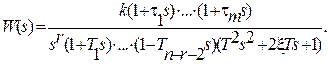 (2.16)
(2.16)
Типовые звенья будут подробно рассмотрены в следующем разделе.
 2014-02-24
2014-02-24 668
668








