2014-02-24
704
Методы линеаризации
В общем случае вектор-функци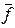и 
и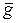 
в уравнениях (2.4) и (2.5) являются нелинейными. Если эти функции удаётся линеаризовать, то изучение подобных нелинейных, но линеаризованных систем, проводятся с применением значительно более простых методов применимых для линейных систем автоматического управления.
Методы линеаризации можно разделить на две группы:
Статическая нелинейность задается функцией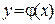 
и может быть представлена графически. Пусть линеаризация проводится при 
, 
, 
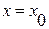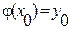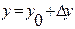. При достаточно малом диапазоне изменения аргумента 
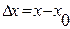справедливо соотношение
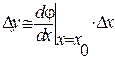, (2.6)
Введя обозначение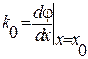 
, получим линейное уравнение относительно новой переменной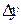 
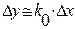. (2.7)
Если диапазон изменения аргумента х функции 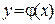настолько велик, что провести линеаризацию на всем диапазоне невозможно, то выбираются несколько значений аргумента 
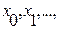определяющие рабочие (опорные) режимы работы системы (или элемента системы). Тогда в достаточно небольшом диапазоне изменения переменной х относительно выбранного рабочего режима 
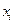получим линеаризованное уравнение (2.7) с коэффициентом 
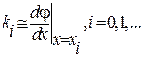. Значения коэффициентов 
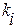при этом могут существенно отличаться друг от друга.
