Использование дисперсионного анализа позволяет ответить на вопрос, оказывает ли существенное влияние некоторый фактор X на исследуемую величину Y. Метод заключается в сравнении дисперсии, возникающей под влиянием факторов X, т.е. факторной дисперсии, с остаточной дисперсией, обусловленной случайными причинами. Если различие между дисперсиями значимо – фактор X существенно влияет на выходной параметр [73].
Дискриминантный анализ [74] используется для принятия решения о том, какие переменные вызывают большие рассеяния выходных величин (различают (дискриминируют) совокупности характеристик оцениваемых объектов). С вычислительной точки зрения дискриминантный анализ аналогичен дисперсионному анализу. Основная идея метода заключается в том, чтобы определить, отличаются ли совокупности по средним значениям той или иной характеристики (или их комбинаций), а затем использовать эту характеристики для классификации объектов по группам. Поскольку при использовании метода обычно имеют дело с несколькими характеристиками, факторами (переменными), задача также состоит в том, чтобы установить, какие из факторов вносят более значимый вклад в различие между совокупностями. Такая методика аналогична процедуре многомерного дисперсионного анализа.
Рассмотрим алгоритм использования дисперсионного анализа:
1. Исходные данные и обозначения.
Метод предполагает использование экспериментальных значений влияющих факторов и выходных параметров:
y – значение выходного параметра;
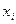 - значения влияющих факторов, их количество N;
- значения влияющих факторов, их количество N;
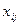 - значение i -го фактора в j -м измерении, количество измерений m;
- значение i -го фактора в j -м измерении, количество измерений m;
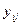 - мгновенное значение выходного параметра под влиянием i -го фактора в j -м измерении.
- мгновенное значение выходного параметра под влиянием i -го фактора в j -м измерении.
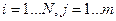
2.Рассчитывают средние значения:
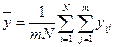 - общее среднее значение выходного параметра;
- общее среднее значение выходного параметра;
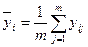 - среднее значение выходного параметра при i -м значении фактора, т.е. значение, усредненное по измерениям.
- среднее значение выходного параметра при i -м значении фактора, т.е. значение, усредненное по измерениям.
3. Рассчитывают дисперсии:
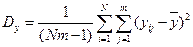 - общая дисперсия;
- общая дисперсия;
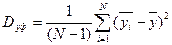 - факторная дисперсия, т.е. разброс значений выходного параметра под влиянием различных факторов;
- факторная дисперсия, т.е. разброс значений выходного параметра под влиянием различных факторов;
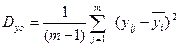 - остаточная дисперсия.
- остаточная дисперсия.
4.Оценка значимости различия дисперсий проводится с помощью критерия Фишера (F-критерия), равного дисперсионному отношению
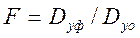 .
.
Влияние фактора X на параметр Y значимо, если 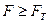 , незначительно, если
, незначительно, если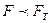 . Значение
. Значение 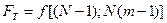 определяют по таблицам (Приложение 1) при заданном уровне значимости.
определяют по таблицам (Приложение 1) при заданном уровне значимости.
 2014-02-24
2014-02-24 670
670








