В общем случае, когда нет аналитической зависимости 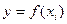 между функцией отклика и влияющими факторами, можно использовать степенной ряд
между функцией отклика и влияющими факторами, можно использовать степенной ряд
 ,
,
где k – число влияющих факторов.
Так как необходимо иметь математическую модель, которую можно использовать для решения реальных практических задач, связанных с анализом результатов измерений, число членов степенного ряда ограничивается и степенной ряд заменяется полиномом некоторой степени. Например, если при двухфакторном эксперименте выходной параметр линейно связан с влияющими факторами, модель, аппроксимирующая экспериментальные результаты, является
- полиномом первой степени
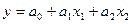 ;
;
если имеет место квадратичная зависимость, необходимо в виде модели принимать
- полином второй степени
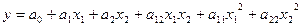 ;
;
модель в виде полинома третьей степени в данном случае будет выглядеть
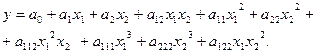
Для аппроксимации зависимости 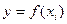 выходного параметра от влияющих факторов можно использовать метод минимальных квадратов,
выходного параметра от влияющих факторов можно использовать метод минимальных квадратов,
Расчет заключается в нахождении функции  , значения которой при
, значения которой при 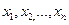 как можно меньше отличаются от экспериментально полученных значений
как можно меньше отличаются от экспериментально полученных значений 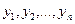 .
.
Как известно, наиболее универсальным выражением для аппроксимации различных зависимостей является полином вида
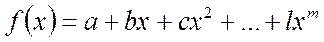 . (3.23)
. (3.23)
Параметры полинома должны быть подобраны таким образом, чтобы cумма квадратов отклонений между экспериментальными и теоретическими значениями была минимальна
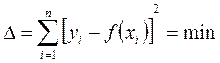 , (3.24)
, (3.24)
где 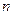 - число экспериментальных результатов
- число экспериментальных результатов 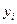 ,
,
При этом частные производные по неизвестным параметрам полинома 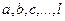 должны быть равны 0:
должны быть равны 0:
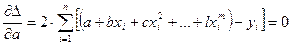
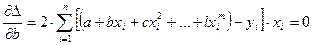 (3.25)
(3.25)
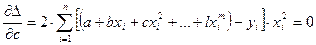
…………………………………………………….
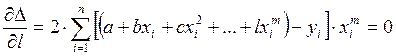 .
.
Методика расчета коэффициентов полинома:
1. По результатам измерения составляют условные уравнения
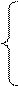
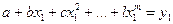
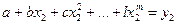 (3.26)
(3.26)
……………………………
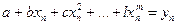 .
.
Число экспериментальных значений 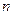 должно быть больше или равно числу неизвестных
должно быть больше или равно числу неизвестных 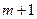 .
.
2. Составляют нормальные уравнения.
Для этого последовательно умножают каждое условное уравнение на коэффициент при неизвестном параметре, складывают условные уравнения:
- коэффициент при параметре 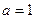 , поэтому первое нормальное уравнение будет иметь вид
, поэтому первое нормальное уравнение будет иметь вид
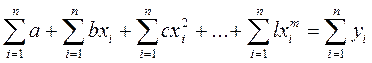 ; (3.27)
; (3.27)
- коэффициент при 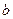 равен
равен 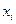 , поэтому второе нормальное уравнение имеет вид
, поэтому второе нормальное уравнение имеет вид
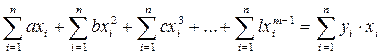 ; (3.28)
; (3.28)
- коэффициент при 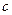 равен
равен 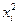 , поэтому третье нормальное уравнение имеет вид
, поэтому третье нормальное уравнение имеет вид
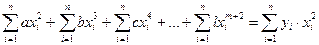 .(3.29)
.(3.29)
Число нормальных уравнений должно быть равно числу искомых параметров.
3. Решают систему нормальных уравнений, находят параметры 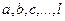 , и получают аппроксимирующее выражение
, и получают аппроксимирующее выражение
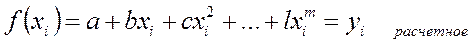 . (3.30)
. (3.30)
Все последующие расчеты позволяют определить погрешность проведенной аппроксимации.
4. По найденному выражению определяют значения 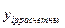 для экспериментальных значений
для экспериментальных значений 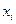 .
.
5. Находят разность 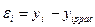 между экспериментальными значениями
между экспериментальными значениями 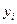 и рассчитанными значениями
и рассчитанными значениями 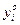 .
.
6. Находят поправки 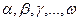 на параметры путем составления новых условных уравнений
на параметры путем составления новых условных уравнений
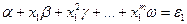
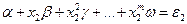 (3.31)
(3.31)
…………………………….
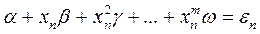
Количество усл.уравнений должно быть равно количеству неизвестных поправок
7. Составляют систему нормальных уравнений, которые получают при умножении последовательно каждого условного уравнения на множители при поправках и при их сложении:
- первое нормальное уравнение: (при умножении на множитель при 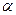 )
)
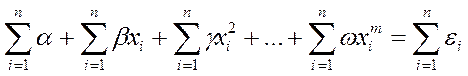 ;
; (3.32)
(3.32)
- второе нормальное уравнение: (при умножении на множитель при 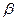 )
)
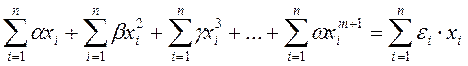 ; (3.33)
; (3.33)
- при умножении на множитель при 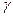
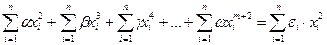 .(3.34)
.(3.34)
и т.д.
Количество нормальных уравнений должно быть равно числу неизвестных поправок на коэффициенты полинома.
Поправки 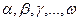 находят при решении системы полученных нормальных уравнений.
находят при решении системы полученных нормальных уравнений.
8. Находят значения коэффициентов полинома (аппроксимирующей функции) с учетом поправок
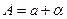
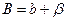
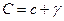 (3.35)
(3.35)
………..
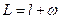 .
.
При этом аппроксимирующая функция (статическая модель) будет иметь вид
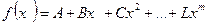 . (3.36)
. (3.36)
9. Определяют погрешность аппроксимации:
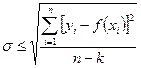 (3.37)
(3.37)
где 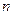 - число условных уравнений (число экспериментальных значений
- число условных уравнений (число экспериментальных значений 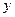 );
); 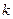 - число коэффициентов полинома.
- число коэффициентов полинома.
В практических задачах могут иметь место частные случаи аппроксимации функциональных параметров:
- Степенная функция вида
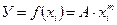 (3.38)
(3.38)
при 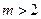 - встречается, например, при резком изменении выходного параметра от эксплуатационного фактора (например, изменение износа металлорежущего инструмента во времени). Для определения
- встречается, например, при резком изменении выходного параметра от эксплуатационного фактора (например, изменение износа металлорежущего инструмента во времени). Для определения
коэффициентов 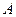 и
и 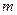 также используется метод наименьших квадратов с приведением уравнения к линейному при помощи логарифмирования
также используется метод наименьших квадратов с приведением уравнения к линейному при помощи логарифмирования
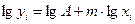 . (3.39)
. (3.39)
По аналогии с предыдущей задачей определяются нормальные уравнения
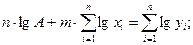
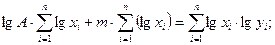 (3.40)
(3.40)
где 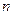 - число экспериментальных данных.
- число экспериментальных данных.
- Экспоненциальная функция
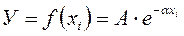 (3.41)
(3.41)
встречается, например, при описании зависимости температурных деформаций режущего инструмента во времени, при описании сенсорных, психофизических зависимостей, характеристик надежности (таких, как вероятность безотказной работы).
В этом случае целесообразно находить не минимальные суммы квадратов отклонений, а минимальные суммы квадратов отклонений логарифмов этих функций
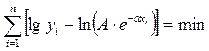 , (3.42)
, (3.42)
т.е.
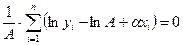
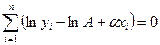 . (3.43)
. (3.43)
Система нормальных уравнений будет иметь вид 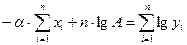 ;
;
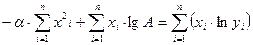 . (3.44)
. (3.44)
 2014-02-24
2014-02-24 1183
1183








