Специфика ЗПР

Основные понятия, используемые в задачах принятия решения

Альтернативы — варианты процедур и действий, среди которых нужно выбрать наилучшие.

Примеры:

Варианты схем с разными параметрами.

Варианты стратегии игры.

Оперирующая сторона — лицо, принимающее решение (ЛПР). ЛПР – это один человек или группа людей или техническая система, определяющая выбор среди альтернатив.

К ЛПР предъявляются следующие требования:

· достаточная объективность и компетентность. Проверяется с помощью тестовых задач с известными заранее ответами;

· устойчивость, однозначность мнений ЛПР при оценки предпочтений. Проверяется сравнением ответов на одни и те же вопросы при изменении порядка их следования, изменения интервала времени между ними и т.д;

· транзитивность оценок ЛПР. Проверяется сравнением предпочтений ЛПР;

Пример:

Пусть предпочтения ЛПР заданы предпочтениями:

А f В А f В

1) B f C 2) B f C

А f С A p C

Оценка транзитивна Оценка не транзитивна

· способность ЛПР к сложному логическому выводу с учетом многих факторов.

Конкурирующая сторона — соперник ЛПР. Если в ЗПР (задача принятия решений) участвует более одного ЛПР, то принятие решений называется игрой, участники — игроками, а задача принятия решений — задачей теории игр.

Конфликт — любое явление или задача с несколькими целями. Почти все задачи конфликтные.

Природа (среда) — одно из действующих лиц — отличается от ЛПР тем, что она неуправляема. Среда характеризуется своим состоянием. В зависимости от имеющихся сведений о состоянии Среды различают три типа ЗПР:

· ЛПР знает полностью состояние Среды. Это — ЗПР в условиях определенности.

· ЛПР знает для каждого состояния Среды вероятность его появления. Это — ЗПР в условиях риска.

· ЛПР ничего не знает о состоянии Среды. Это — ЗПР в условии неопределенности.

ЗПР – это не обычные задачи решения уравнений или вычислений по формулам или алгоритмам. При решении ЗПР возникают следующие специфические проблемы.

1. Проблема многокритериальности состоит в том, что обычно решение характеризуется не одним, а несколькими частными критериями, и необходимо охарактеризовать эту группу критериев одним числом. Обычно проблема решается выбором одного из частных критериев в качестве главного и переводом остальных в разряд ограничений или в замене группы частных критериев каким-либо обобщённым критерием, то есть одной из возможных комбинаций этих критериев. Например, микросхему, характеризуемую несколькими частными критериями, можно охарактеризовать аддитивным критерием в виде их взвешенной суммы (см. раздел 1.3 пункт Б).

2. Проблема конфликтности. Пусть имеются два критерия Y1(x), Y2(x), зависящих от одной и той же переменной x. Проблема конфликтности заключается в том, что оптимальные значения критериев Y1 и Y2 получаются при разных значениях х (см. рисунок). Улучшение значения критерия Y2(x) ведёт к ухудшению значения критерия Y1(x) и наоборот – в этом заключается конфликт этих критериев. Одновременно получить наилучшие значения обоих критериев нельзя.

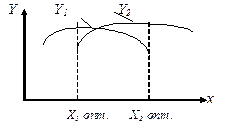
Преодоление конфликта возможно путем объединения Y₁ и Y₂ в составе обобщенного критерия: Y=K₁*Y₁+K₂*Y₂. Сумма критериев принимает оптимальное значение при оптимальном соотношении вкладов в неё каждого критерия.

3. Проблема понимания оптимальности. Задача ЛПР при решении ЗПР состоит в выборе лучшей альтернативы. При этом нужно иметь в виду, что объективного оптимального решения ЗПР, устраивающего всех ЛПР, решающих данную задачу, не существует. В отличие от строгих математических задач, имеющих точный и однозначный ответ, задачи принятия решения таких однозначных ответов не имеют. Количество ответов бесконечно велико и каждый из них будет правильным для каждого ЛПР в зависимости от выбора им типа обобщённого критерия оптимальности и весовых коэффициентов в этих критериях. ЛПР может, составлять обобщенный критерий Y по-разному, исходя из своей субъективной точки зрения. Например, лучшие альтернативы, выбранные по критериям:

Y=K1*Y1+K2*Y2 или Y=(K1*Y1)*(K2*Y2)

могут быть разными. Кроме того, разные ЛПР могут выбрать не только разные обобщённые критерии, но и разные весовые коэффициенты K1, K2, исходя из своего понимания важности критериевY1, Y2 –.чем важнее критерии, тем больше значение коэффициента. Поэтому понятие оптимальности является субъективным.. Каждый счастлив по-своему!. Математическую задачу, сколько будет два плюс два, все нормальные люди решат одинаково, но задачу принятия решений, что лучше: быть бедным и здоровым или быть богатым и больным, каждый решит по-своему, в зависимости от своих приоритетов и взглядов на жизнь. Ответы будут разными. Поэтому решения ЗПР оптимальны лишь условно, относительно.

Понятие оптимального решения ЗПР зависит также от смысла понятия “оптимум”. 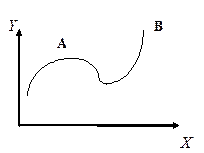Рассмотрим, например, такую функцию (см. рисунок). Смысл понятия “точка оптимума” на этом графике определяется смыслом переменных X и Y. Пусть Y — доход, а X — расход. Точки оптимума будут разными для понятий X — неограниченный расход времени для получения максимального дохода (точка В) и X — ограниченный расход здоровья для получения дохода (точка А), так как для получения дохода, соответствующего точке В, здоровья может не хватить).

4. Проблема нечеткости. ЛПР приходится принимать решение при неполной, неопределённой или нечёткой информации. Под нечёткостью в данном случае понимается неоднозначность. Например, нет однозначности при решении вопроса о значениях весовых коэффициентов или выборе вида обобщённого критерия или при определении предпочтений между качественными критериями. В этом случае для получения недостающей информации приходится прибегать к экспертизе. Экспертиза — опрос одного или нескольких экспертов, которые выставляют оценки (весовые коэффициенты) частным критериям или определяют предпочтения критериев или объектов. Кроме того, нет определённости в случае отсутствия информации о состоянии окружающей среды. Далее мы рассмотрим в основном задачи определения альтернатив, характеризующихся своими параметрами, в качестве которых выступают значения частных или обобщённых критериев.

Теория принятия решений, несмотря на неоднозначность получаемых решений из-за их субъективности, эффективна и необходима, так как она позволяет:

· правильно поставить задачу поиска оптимума и записать ее формально;

· изучить типовые ситуации при принятии решений;

· не принимать ошибочных решений и не искать наилучшее решение там, где его не существует;

· изучить методы принятия относительно оптимальных решений

· быть уверенным в том, что принятое вами решение оптимально именно для вас с вашим личным пониманием оптимальности.