1. Рефлексивность. Отношение 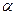 на множестве А рефлексивно, если каждый элемент множества А находится в отношении
на множестве А рефлексивно, если каждый элемент множества А находится в отношении 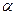 с самим собой, т.е.
с самим собой, т.е.
(a, a) 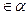 для
для 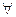 a
a 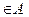
Графически это означает
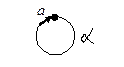
В таблице булевой матрицы отношений рефлексивность выражается в том, что все диагональные клетки равны единице.
Пример: Отношение равенства на множестве чисел рефлексивно, так как каждое число равно самому себе.
2. Антирефлексивность. Если отношение (а, а) 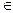
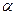 не имеет места ни для одного элемента множества А, то
не имеет места ни для одного элемента множества А, то 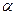 — антирефлексивное отношение.
— антирефлексивное отношение.
Пример:
Отношение “больше” антирефлексивно на можестве действительных чисел, так как каждое число не может быть больше самого себя.
3. Симметричность. Если для всех пар, принадлежащих отношению 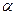 , справедливо, что если из (a, b)
, справедливо, что если из (a, b) 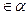 следует, что (b, a)
следует, что (b, a) 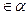 , то
, то 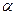 — симметричное отношение.
— симметричное отношение.
Графически симметричность обозначается: 
Таблично симметричность выражается симметрией булевой матрицы отношений относительно главной диагонали.
4. Ассимметричность. Отношение 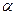 ассиметрично, если для всякой пары (a, b)
ассиметрично, если для всякой пары (a, b) 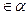 обратная пара (b, a)
обратная пара (b, a) 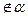 .
.
Пример:
Отношение равенства на множестве действительных чисел симметрично, а отношения “больше” и “меньше” ассиметричны. Отношение “больше-равно” содержит как симметричную, так и ассиметричную части.
5. Транзитивность. Отношение 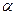 транзитивно, если из условия: пара (a, b)
транзитивно, если из условия: пара (a, b) 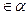 и пара (b,c)
и пара (b,c) 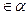 следует, что пара (a, c)
следует, что пара (a, c) 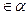 .
.
Графически транзитивность пары (a, c) обозначается
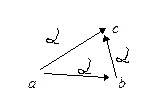
 2014-02-24
2014-02-24 759
759







