Системы массового обслуживания

Раздел 3. ЗАДАЧИ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ

В системах массового обслуживания различают три основ­ных этапа, которые проходит каждая заявка:

• появление заявки на входе в систему;

• прохождение очереди;

• процесс обслуживания, после которого заявка покидает си­стему.

На каждом этапе используются определенные характеристики, которые следует обсудить прежде, чем строить математические модели.

Характеристики входа

Вход в любую систему массового обслуживания имеет три основные характеристики:

• число заявок на входе (размер популяции);

• режим поступления заявок в систему обслуживания;

• поведение клиентов.

Число потенциально возможных заявок (размер популяции) может считаться либо бесконечным (неограниченная популяции либо конечным (ограниченная популяция). Если число заявок, поступивших на вход системы с момента начала процесса обслу­живания до любого заданного момента времени является лини малой частью потенциально возможного числа клиентов, попу­ляция на входе рассматривается как неограниченная. Примерам неограниченных популяций могут служить автомобили, проходящие через пропускные пункты на скоростных дорогах, покупатели в супермаркете. В большинстве моделей очередей на входе рассматриваются именно неограниченные популяции.

Если число заявок, которое может поступить в систему, срав­нимо с числом заявок, уже находящимся в системе массового обслуживания, популяция считается ограниченной. Примеров ограниченной популяции могут служить компьютеры, принад­лежащие конкретной организации и поступающие на обслужи­вание в ремонтную мастерскую.

Режим поступления в систему

Заявки могут поступать в систему обслуживания в соответствии с определенным графиком (один пациент на прием к стоматологу каждые пятнадцать минут, один автомобиль на кон­вейере каждые двадцать минут), или они появляются случайный

образом. Появления клиентов считаются случайными, если они независимы друг от друга и точно не предсказуемы. Часто в за­дачах массового обслуживания число появлений в единицу вре­мени может быть оценено с помощью распределения вероятно­стей, известного, как пуассоновское распределение. При задан­ном темпе поступления (например, два клиента в час, или четыре грузовика в минуту), дискретное распределение Пуассона опи­сывается следующей формулой:

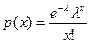для х = 0, 1, …,

где р(х) — вероятность поступления х заявок в единицу времени;

х —число заявок в единицу времени;

λ— среднее число заявок в единицу времени (темп поступ­ления заявок);

е = 2,7183 (основание натурального логарифма).

Соответствующие значения вероятностей р(х) нетрудно оп­ределить с помощью таблицы пуассоновского распределения. Например, если средний темп поступления заявок равен двум клиентам в час, то вероятность не поступления в систему в те­чение часа ни одной заявки равна 0,13; вероятность появления одной заявки -0,27; двух — также около 0,27; три заявки могут появиться с вероятностью 0,18; четыре — с вероятностью около 0,9 и т.д. Вероятность того, что за час в систему поступят 9 и более заявок близка нулю.

На практике вероятности появления заявок не всегда под­чиняются пуассоновскому распределению. Поэтому, сначала следует провести предварительное исследование, будет ли пуас­соновское распределение давать хорошую аппроксимацию для данного процесса.