КОНТРОЛЬНЫЕ ВОПРОСЫ 5
КОНТРОЛЬНЫЕ ВОПРОСЫ 4
Задача оптимизации перевозок однородного продукта
Задача распределения грузов по средствам доставки
КОНТРОЛЬНЫЕ ВОПРОСЫ 3
Задача распределения количества заказов по предприятиям
Пусть имеется m видов заказов в количестве 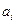 единиц,
единиц, 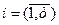 . Для их выполнения определены n предприятий с располагаемыми ресурсами
. Для их выполнения определены n предприятий с располагаемыми ресурсами 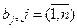 на выполнение заказов. Введём обозначения:
на выполнение заказов. Введём обозначения: 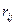 – количество ресурсов, затраченных j -м предприятием на изготовление единицы i- го заказа,
– количество ресурсов, затраченных j -м предприятием на изготовление единицы i- го заказа, 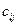 – стоимость изготовления на j- м предприятии единицы i -го заказа,
– стоимость изготовления на j- м предприятии единицы i -го заказа, 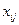 – количество изделий i- го заказа выпускаемых на j- м предприятии.
– количество изделий i- го заказа выпускаемых на j- м предприятии.
Требуется распределить имеющиеся заказы по выделенным предприятиям так, чтобы суммарная стоимость их выполнения была минимальна, при условии выполнения всех заказов при наличных ресурсах.
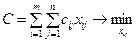 . (4.8)
. (4.8)
Условие того, что все заказы будут выполнены, примет вид:
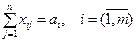 . (4.9)
. (4.9)
Ограничение на ресурсы, имеющиеся на предприятии:
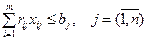 . (4.10)
. (4.10)
На переменные 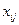 данной ММ должны быть наложены условия целочисленности:
данной ММ должны быть наложены условия целочисленности:
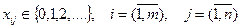 . (4.11)
. (4.11)
Задача (4.8)-(4.11) является однокритериальной задачей линейного дискретного программирования и может быть решена методом ветвей и границ или методом отсечений. Потребуем, чтобы все заказы на предприятии были выполнены за минимальное время. Введём переменную 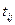 – затраты времени на выполнение единицы i -го заказа на j- м предприятии. Тогда второй критерий оптимальности распределения заказов на предприятии можно записать:
– затраты времени на выполнение единицы i -го заказа на j- м предприятии. Тогда второй критерий оптимальности распределения заказов на предприятии можно записать:
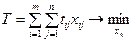 . (4.12)
. (4.12)
Получим ещё одну однокритериальную ММ вида (4.12),(4.9)–(4.11). Двухкритериальные модели оптимального распределения заказов по предприятиям определяется выражениями (4.8), (4.12), (4.9) - (4.11).
1. Сформулируйте задачу выбора оптимальной производственной программы предприятия.
2. Приведите математическую модель суммарной прибыли от реализации всей продукции.
3. Приведите математическую модель общих затрат времени на выпуск запланированной продукции.
4. Приведите математическую модель численности работников, участвующих в изготовлении продукции.
5. Какие особенности имеют распределительные задачи ПР?
6. Приведите математическую модель суммарной стоимости выполнения заказов при распределении их по выделенным предприятиям.
7. Приведите математическую модель суммарных затрат времени на выполнение заказов предприятиями.
8. Сформулируйте задачу распределения грузов по средствам доставки.
9. Приведите математическую модель суммарных затрат времени на погрузку грузов на имеющиеся транспортные средства.
10. Приведите математическую модель суммарной стоимости выполнения всех погрузочных работ.
11. Приведите математическую модель общие затраты на аренду дополнительных средств доставки.
|
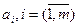 . Для их перевозки можно использовать n транспортных единиц (автомобиль, самолет, вагон и т.д.) в количестве
. Для их перевозки можно использовать n транспортных единиц (автомобиль, самолет, вагон и т.д.) в количестве 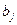 единиц,
единиц, 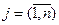 . Известно, что в единицу j- го транспортного средства помещается
. Известно, что в единицу j- го транспортного средства помещается 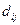 единиц груза. При этом время погрузки единицы i -го груза j- м транспортным средством составляет
единиц груза. При этом время погрузки единицы i -го груза j- м транспортным средством составляет 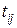 единиц времени.
единиц времени.
Требуется распределить имеющиеся транспортные средства под имеющиеся грузы так, чтобы суммарные затраты времени на их погрузку были минимальными при условии отправки всех имеющихся грузов и ограничений на вместимость имеющихся транспортных средств. Пусть 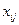 – количество j- х транспортных средств доставки, выделяемых под грузы i- го вида. Тогда общие затраты времени на погрузку всех грузов
– количество j- х транспортных средств доставки, выделяемых под грузы i- го вида. Тогда общие затраты времени на погрузку всех грузов
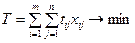 . (4.13)
. (4.13)
Условие ограничения по числу использованных транспортных средств доставки 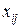 по всем видам груза примет вид:
по всем видам груза примет вид:
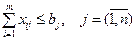 . (4.14)
. (4.14)
Условие погрузки и отправки всех имеющихся грузов:
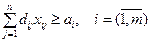 . (4.15)
. (4.15)
Добавим естественное ограничение вида
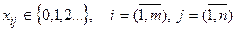 . (4.16)
. (4.16)
Выражения (4.13) - (4.16) описывают классическую однокритериальную линейную дискретную задачу.
В качестве дополнительной целевой функции будем использовать суммарную стоимость выполнения всех погрузочных работ:
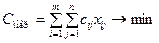 . (4.17)
. (4.17)
Здесь 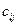 – стоимость погрузки
– стоимость погрузки 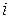 -го вида груза в одно j -е средство доставки. Тогда выражения (4.13), (4.17), (4.14) - (4.16) описывают двухкритериальную задачу.
-го вида груза в одно j -е средство доставки. Тогда выражения (4.13), (4.17), (4.14) - (4.16) описывают двухкритериальную задачу.
Если решение сформулированной задачи не существует по причине небольшого количества средств доставки, последние могут быть арендованы у сторонних организаций.
Введем обозначение 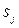 – стоимость аренды одного средства доставки j -го вида,
– стоимость аренды одного средства доставки j -го вида,
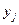 – количество арендованных средств j -го вида, где:
– количество арендованных средств j -го вида, где:
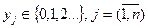 . (4.18)
. (4.18)
Тогда общие затраты на аренду дополнительных средств доставки могут быть записаны как:
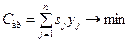 . (4.19)
. (4.19)
Переменные 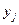 связаны с ограничением (4.14) соотношением вида:
связаны с ограничением (4.14) соотношением вида:
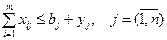 .
.
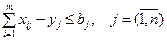 . (4.20)
. (4.20)
Получим трехкритериальную модель, описываемую выражениями (4.13), (4.17), (4.19), (4.20), (4.14), (4.15), (4.16), (4.18).
Эта задача является одной из важных задач в оптимизационной деятельности организационно-технических систем. Одной из первых задач оптимизации перевозок явилась классическая транспортная задача (КТЗ).
Основные предположения КТЗ:
1) потребности пунктов назначения перевозок груза удовлетворяются за счёт нескольких пунктов его отправления,
2) величина транспортных расходов при перевозке груза пропорциональна количеству перевозок по каждому маршруту.
Пусть имеется однородная продукция, сосредоточенная у m поставщиков в объёмах соответственно 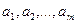 . Этот продукт необходимо доставить n потребителям, которые имеют потребности в нём, равные
. Этот продукт необходимо доставить n потребителям, которые имеют потребности в нём, равные 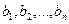 . Пусть заданы
. Пусть заданы 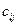 – стоимость перевозки единицы продукта от i- го поставщика j- му потребителю
– стоимость перевозки единицы продукта от i- го поставщика j- му потребителю 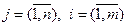 . Требуется определить величины
. Требуется определить величины 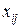 объёмов продукта, перевозимого от i- го поставщика j- му потребителю. Транспортная задача графически представлена на рис. 4.3.
объёмов продукта, перевозимого от i- го поставщика j- му потребителю. Транспортная задача графически представлена на рис. 4.3.
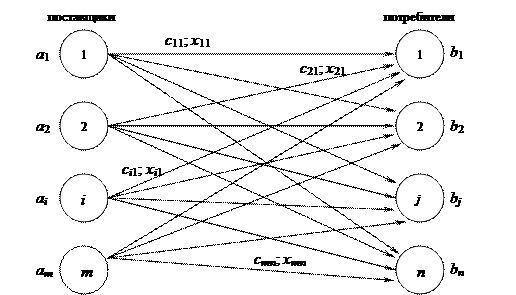
Рис. 4.3
Все маршруты перевозок являются возможными.
Будем считать, что запасы и потребности в системе сбалансированы:
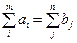 . (4.21)
. (4.21)
Переменные 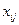 в этом случае должны удовлетворять ряду условий.
в этом случае должны удовлетворять ряду условий.
Запасы всех поставщиков должны быть вывезены:
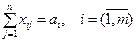 . (4.22)
. (4.22)
Все потребности в системе должны быть удовлетворены:
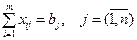 . (4.23)
. (4.23)
Условие того, что не все маршруты перевозок могут быть реализованы:
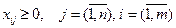 . (4.24)
. (4.24)
Суммарная стоимость всех перевозок с учетом транспортных расходов вычисляется как:
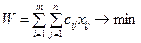 . (4.25)
. (4.25)
КТЗ формулируется в следующем виде: требуется определить значение переменных 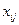 , доставляющих минимум целевой функции (4.25) при выполнении ограничений (4.21) - (4.24). Видно, что данная модель является линейной моделью ЗПР. Модель (4.25), (4.21) - (4.24) при наличии условия (4.21) называется закрытой транспортной задачей по критерию стоимости.
, доставляющих минимум целевой функции (4.25) при выполнении ограничений (4.21) - (4.24). Видно, что данная модель является линейной моделью ЗПР. Модель (4.25), (4.21) - (4.24) при наличии условия (4.21) называется закрытой транспортной задачей по критерию стоимости.
В реальных задачах условие (4.21) часто нарушается. Рассмотрим два возможных случая:
1. Сумма запасов превышает сумму потребностей данной продукции
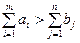 . (4.27)
. (4.27)
Так как в этом случае все запасы не могут быть вывезены, то условие (4.22) заменяется условием вида:
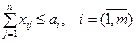 . (4.28)
. (4.28)
2. Сумма потребностей превышает сумму запасов:
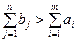 . (4.29)
. (4.29)
В этом случае часть потребностей не удастся удовлетворить, поэтому ограничение вида (4.23) заменяется неравенством:
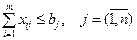 . (4.30)
. (4.30)
Математические модели вида (4.25), (4.23), (4.28), (4.24) и (4.25), (4.22), (4.30), (4.24) описывают открытые транспортные задачи. Как закрытые, так и открытые транспортные задачи являются задачами линейного программирования и могут быть решены соответствующими численными методами. Однако, если размерность задачи слишком велика (для больших 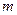 и
и 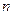 ), то эти методы являются весьма трудоемкими. Однако для закрытой транспортной задачи (ТЗ) имеются свои более простые методы решения, в которых используется табличная форма представления исходных данных.
), то эти методы являются весьма трудоемкими. Однако для закрытой транспортной задачи (ТЗ) имеются свои более простые методы решения, в которых используется табличная форма представления исходных данных.
С учетом сказанного, рассмотрим методы сведения открытой КТЗ к закрытой КТЗ.
1. Пусть в системе выполняются условия вида (4.27) в этом случае вводится фиктивный (n +1) потребитель, с потребностью равной:
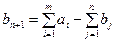 ,
,
но, так как данного потребителя в системе нет, то стоимость перевозки к нему от всех поставщиков полагается равной 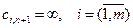 .
.
2. Пусть в системе выполняется условие вида (4.29). В этом случае вводится фиктивный (m +1) поставщик с запасом, равным
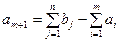 ,
,
соответственно стоимость перевозки от этого поставщика ко всем потребителям полагается равной 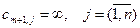 .
.
Вследствие вида критерия (4.25) и бесконечной стоимости перевозок при 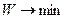 автоматически обнуляются переменные
автоматически обнуляются переменные 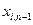 и
и 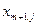 . При практических расчетах коэффициенты
. При практических расчетах коэффициенты 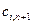 и
и 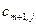 обычно полагают равными очень большим числам, на несколько порядков выше, чем реальный
обычно полагают равными очень большим числам, на несколько порядков выше, чем реальный 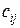 . Аналогичным образом с помощью коэффициентов
. Аналогичным образом с помощью коэффициентов 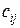 можно ввести запрещающий маршрут и в закрытой КТЗ.
можно ввести запрещающий маршрут и в закрытой КТЗ.
Рассмотрим свойства классической транспортной задачи. Задача (4.25), (4.21) -(4.24), как задача линейного программирования специального типа имеет следующие особенности:
1) Все коэффициенты при xij в ограничениях (4.22) и (4.23) равны 1.
2) Система ограничений (4.22), (4.23) включает в себя 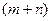 уравнений.
уравнений.
3) Ранг системы (4.22), (4.23) вследствие (4.21) равен 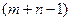 . Это означает, что оптимальное решение задачи (4.25), (4.21)-(4.24) будет содержать
. Это означает, что оптимальное решение задачи (4.25), (4.21)-(4.24) будет содержать 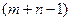 ненулевых объемов перевозок.
ненулевых объемов перевозок.
Докажем, что любая закрытая ТЗ имеет решение.
Конкретизируем условие (4.21) в следующем виде:
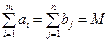 , (4.31)
, (4.31)
где 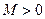 , величина суммарного объема запасов и потребностей в системе.
, величина суммарного объема запасов и потребностей в системе.
Выберем объем перевозок в системе по формуле
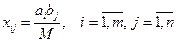 . (4.32)
. (4.32)
Покажем, что решение вида (4.32) является допустимым решением задачи (4.25), (4.21) - (4.24).
Подставив величину (4.32) в выражение (4.22), (4.23) получим подтверждение условий (4.22), (4.23) при выбранном решении. Условие (4.24) выполняется очевидным образом, так как все 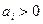 и
и 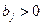 . Отсюда следует, что допустимое множество решений задачи (4.25), (4.21) - (4.24) не пустое, так как содержит хотя бы одну точку вида (4.32).
. Отсюда следует, что допустимое множество решений задачи (4.25), (4.21) - (4.24) не пустое, так как содержит хотя бы одну точку вида (4.32).
Покажем, что целевая функция (4.25) ограничена. Выберем в матрице стоимости перевозок 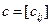 максимальный и минимальный элемент
максимальный и минимальный элемент 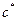 ,
, 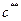 . Внесем в матрицу
. Внесем в матрицу 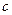 сначала
сначала 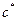 , а затем
, а затем 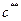 и посчитаем при этом значение целевой функции
и посчитаем при этом значение целевой функции 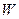 для выбранного решения (4.32). В итоге получим следующее двойное неравенство, свидетельствующее об ограниченности целевой функции
для выбранного решения (4.32). В итоге получим следующее двойное неравенство, свидетельствующее об ограниченности целевой функции 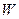 сверху и снизу:
сверху и снизу: 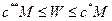 .
.
1. Сформулируйте классическую транспортную задачу.
2. Как выглядит КТЗ графически?
3. Приведите математическую модель суммарной стоимости перевозок.
4. Приведите отличия закрытой и открытой КТЗ.
5. Как решаются открытые КТЗ?
6. Докажите, что КТЗ имеет хотя бы одно ненулевое решение.
7. Докажите, что целевая функция стоимости перевозок ограничена.
4.2.4. Метод минимальной стоимости для решения закрытой
транспортной задачи
|
Исходные данные для решения задачи записываются в табличной форме.
Например, для т = 4, п = 5 исходная таблица стоимости перевозок может быть записана в следующем виде (в нижнем левом углу каждой ячейки будет записываться решение).
| сij xij | 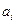 (Запасы) (Запасы)
| |||||
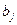 (Заявки) (Заявки)
|
Содержательная постановка задачи. Имеется m пунктов производства некоторой однородной продукции с объемом производства ai единиц в i -м пункте, 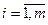 , и n пунктов потребления данной продукции с объемом потребления bj единиц в j -м пункте,
, и n пунктов потребления данной продукции с объемом потребления bj единиц в j -м пункте, 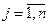 . Суммарные объемы производства и потребления продукции равны:
. Суммарные объемы производства и потребления продукции равны:
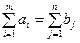 .
.
Перевозка продукции возможна из любого пункта производства в любой пункт потребления, при этом стоимость перевозки единицы продукции из i -го пункта производства в j -й пункт потребления равна cij.
Требуется распределить продукцию из пунктов производства по пунктам потребления таким образом, чтобы суммарная стоимость перевозки была минимальной при условии вывоза всей продукции из пунктов производства и удовлетворения всех запросов пунктов потребления.
Алгоритм эвристического метода включает в себя следующие этапы:
1) Формируется таблица с заданными ai, bj, cij и с начальными нулевыми объемами перевозимой продукции (xij) m ´ n – распределительная таблица.
2) В таблице стоимости перевозок (без учета «вычеркнутых» строк и столбцов) выполняется поиск минимального элемента (ячейки таблицы с минимальной стоимостью перевозок). Пусть это будет ячейка (e, f) с элементом cef – стоимостью перевозки продукции из пункта производства e в пункт потребления f.
3) Возможны три случая:
a. Если ae < bf, то потребность пункта потребления bf уменьшается на ae, строка e «вычеркивается», т.к. вся продукция из пункта производства вывозится полностью: xef = ae, bf = bf – ae, ae = 0;
b. Если ae > bf, то ресурс пункта производства ae уменьшается на bf, столбец f «вычеркивается», т.к. потребность пункта потребления удовлетворяется полностью: xef = bf, ae = ae – bf, bf = 0;
c. Если ae = bf, то используется, либо случай a, либо случай b. Если выбирается случай а, считают, что потребность пункта потребления bf = 0 должна быть полностью удовлетворена. Если же выбирается случай b, полагают, что ресурс пункта производства ae = 0 должен быть полностью вывезен.
4) «Вычеркнутая» строка или столбец далее на этапе 2 не используется.
5) Если вычеркнуты не все строки и столбцы, то переходят к п. 2.
6) Завершить работу алгоритма.
Решение, полученное с помощью данного метода, отличается от точного решения по значению критерия оптимальности 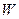 на 5-15%, что вполне приемлемо для практики.
на 5-15%, что вполне приемлемо для практики.
Пример. Примером может служить модель производства и доставки кирпича с кирпичных заводов на стройки республики.
Пусть имеется 3 кирпичных завода (m = 3) и 4 крупные стройки (n = 4).
Производственные мощности каждого завода равны соответственно 10, 20 и 30 тонн кирпича в смену, т.е. а 1 = 10, а 2 = 20, а 3 = 30. Потребности строек составляют 30 т., 10 т., 15 т., 5 т. кирпича в смену, т.е. b 1 = 30, b 2 = 10, b 3 =15, b 4 = 5.
Определить оптимальные количества перевозимого кирпича с каждого завода на четыре стройки из условия минимума суммарной стоимости поставок.
Исходная таблица стоимостей перевозок:
| Стройки Заводы | 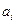
| ||||
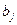
|
Математическая модель суммарной стоимости перевозок:
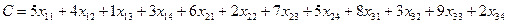 .
.
Согласно алгоритму находим ячейку с наименьшей стоимостью: ячейка 1-3, для нее а 1 = 10 < b 3 = 15, т.о. весь кирпич первого завода будет направлен на третью стройку, потребность третьей стройки уменьшится на 15 – 10 = 5 т., следовательно, в ячейку 1-3 записываем x 13 = 10, вычеркиваем первую строку, b 3 стало равно 5. В оставшейся части таблицы ячейки с наименьшим значением стоимости – 2-2 и 3-4, выбираем 2-2:
| Стройки Заводы | 
| ||||
|
а 2 = 20 > b 2 = 10 Þ x 22 = 10 – вторая стройка полностью может быть обеспечена кирпичом со второго завода, на котором осталось а 2 = 20 – 10 = 10, второй столбец вычеркиваем. Следующая ячейка с наименьшей стоимостью 3-4:
| Стройки Заводы | 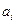
| ||||
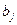
|
И т.д.
| Стройки Заводы | 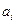
| ||||
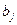
|
| Стройки Заводы | 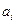
| ||||
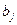
|
| Стройки Заводы | 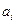
| ||||
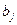
|
Оставшиеся 5т. кирпича с 3-го завода будут направлены на третью стройку.
Таким образом, получили следующее решение:
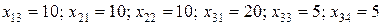 ,
,
которое можно представить в виде графа (рис. 4.3').
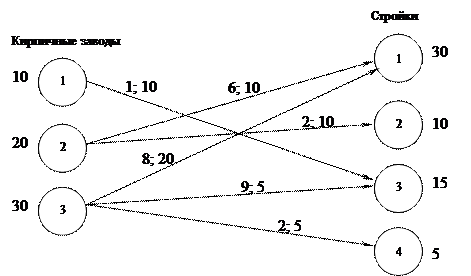
Рис. 4.3'
Суммарная стоимость перевозок составила
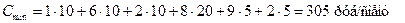
1. Приведите алгоритм эвристического метода закрытой КТЗ.
2. Приведите граф решенной транспортной задачи о кирпичных заводах и стройках.
4.2.5. Пример решения задачи линейного целочисленного
программирования
|
Предприятие может выпускать изделия двух типов: A и B. Весь процесс производства разбит на 4 этапа. Для обоих типов изделий известны затраты времени на каждом из этапов для производства одного изделия, действительный фонд времени для каждого этапа и прибыль от реализации одного изделия каждого типа:
| Показатели (на одно изделие) | Затраты времени, мес. | Фонд времени, мес. | |
| Тип A | Тип B | ||
| 1-й этап | 0,01 | 0,03 | 0,25 |
| 2-й этап | 0,03 | 0,01 | 0,15 |
| 3-й этап | 0,04 | 0,05 | 0,45 |
| 4-й этап | 0,01 | 0,01 | 0,15 |
| Прибыль, руб. |
Требуется найти объёмы выпуска изделий, исходя из следующих условий: прибыль от реализации максимальна, изделий типа A надо выпустить не более 20 шт., а типа B – не менее 7 шт.
Пусть x 1 и x 2 – объёмы выпуска изделий типов A и B соответственно.
Прибыль от реализации изделий составит (целевая функция)
F (x 1, x 2) = 200· x 1 + 240· x 2 ® 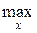 . (1.1)
. (1.1)
Учёт фонда времени по всем этапам приводит к системе неравенств
(ограничения)
0,01· x 1 + 0,03· x 2 ≤ 0,25,
0,03· x 1 + 0,01· x 2 ≤ 0,15, (1.2)
0,04· x 1 + 0,05· x 2 ≤ 0,45,
0,01· x 1 + 0,01· x 2 ≤ 0,15.
Ограничения на число изделий записывается в виде
x 1 ≤ 20, (1.3)
x 2 ≥ 7.
При этом объёмы выпуска изделий должны быть неотрицательными и целочисленными величинами, что определяется их физическим смыслом:
x 1, x 2 ≥ 0, (1.4)
x 1, x 2 – целые.
Для упрощения расчётов умножим на 100 левую и правую части неравенств (1.2):
1· x 1 + 3· x 2 ≤ 25,
3· x 1 + 1· x 2 ≤ 15, (1.5)
4· x 1 + 5· x 2 ≤ 45,
1· x 1 + 1· x 2 ≤ 15.
Таким образом, выражения (1.1), (1.5), (1.3), (1.4) представляют собой математическую модель задачи линейного целочисленного программирования.
Решение сформулированной задачи.
Для решения задачи воспользуемся программой LDPTechs.exe.
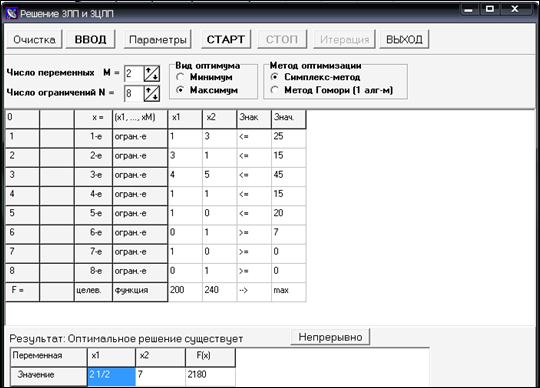
Рис. 1.1
Результат решения данной задачи симплекс-методом имеет вид
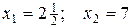 ,
,
при этом значение прибыли равно
F (x 1, х 2) = 2180.
Округление решения.
Каждое из дробных значений результата нужно округлить в меньшую и в большую сторону, проверяя полученное округлённое решение на выполнение ограничений ЗЛП. В нашем случае такое значение одно – это значение переменной x 1, равное 2,5.
1. Округлим дробное значение в меньшую сторону:
x 1» 2, x 2 = 7.
Подставим в неравенства полученные значения:
1· x 1 + 3· x 2 = 1·2 + 3·7 = 23 ≤ 25,
3· x 1 + 1· x 2 = 3·2 + 1·7 = 13 ≤ 15,
4· x 1 + 5· x 2 = 4·2 + 5·7 = 43 ≤ 45,
1· x 1 + 1· x 2 = 1·2 + 1·7 = 9 ≤ 15.
Прибыль от реализации равна
F (x 1, х 2) = 200·2 + 240·7 = 2080.
2. Округлим значение в большую сторону:
x 1» 3, x 2 = 7.
Тогда получим
1· x 1 + 3· x 2 = 1·3 + 3·7 = 24 ≤ 25,
3· x 1 + 1· x 2 = 3·3 + 1·7 = 16 ≤/ 15,
4· x 1 + 5· x 2 = 4·3 + 5·7 = 47 ≤/ 45,
1· x 1 + 1· x 2 = 1·3 + 1·7 = 10 ≤ 15.
В этом случае второе и третье ограничения модели не выполняются. Поэтому данный вариант округления не подходит и дальнейшие расчёты по этому округлению можно не проводить.
Результат решения задачи.
Таким образом, получаем целочисленное оптимальное решение задачи
x 1 = 2, x 2 = 7, F (x 1, х 2) = 2080.
Объёмы выпуска изделий типов A и B должны быть равны 2 шт. и 7 шт. соответственно, при этом прибыль от реализации этих изделий составит 2 080 руб.
С помощью 1-го алгоритма Гомори метода отсечения можно получить точное целочисленное решение задачи.
В результате получим сразу целочисленное решение (рис. 1.5).
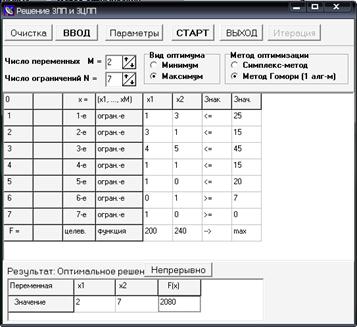
Рис. 1.5
 2014-02-09
2014-02-09 943
943








