Нелинейные модели задач принятия решений

КОНТРОЛЬНЫЕ ВОПРОСЫ 7

Задача оптимального выбора выполняемых работ

Задача о ранце

Задача оптимального выбора

Лекция 7

Во многих случаях применения ТПР рассматривают следующие задачи. Имеется множество объектов (предметов, процессов, проектов, зданий и т.д.), требуется выбрать из этого множества оптимальное подмножество объектов, удовлетворяющих заданному требованию.

Пусть в распоряжении ЛПР имеется 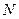объектов. Факт выбора или не выбора j -го объекта осуществляется с помощью переменной

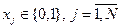. (4.43)

На выбор объекта обычно накладываются технические, экономические и другие ограничения, которые в общем виде записываются как

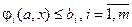, (4.44)

где 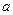и 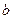– вектора неуправляемых факторов,

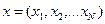– вектор искомых переменных вида (4.43).

Мощность искомого подмножества объектов может быть как ограниченной так и не ограниченной, в частности, если это подмножество должно включать не более 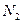и не менее 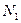элементов, то

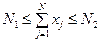. (4.45)

Если по условию задачи необходимо выбрать из 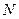элементов только один элемент, то условие (4.45) примет вид:

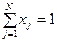. (4.46)

Формирование оптимального множества объектов осуществляется с помощью скалярной или векторной целевой функции (один или много критериев), которая записывается как:

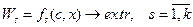. (4.47)

Таким образом, выражения (4.47), (4.45), (4.44), (4.43) описывают многокритериальную, нелинейную, дискретную модель задачи оптимального выбора. При 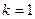получим однокритериальную модель решаемой задачи. В настоящее время на практике в основном используют однокритериальные линейные модели. Рассмотрим примеры задач оптимального выбора.

Имеется ранец объемом b. Дано N предметов, при этом j- й предмет имеет ценность 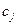и объем a_j, . Требуется определить, какие предметы следует загрузить в ранец, чтобы суммарная ценность предметов была максимальной при ограничении на допустимый объем ранца.

Из постановки задачи следует, что она имеет смысл при .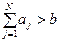

Пусть 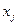– признак загрузки j- го предмета в ранец, .

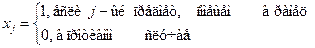
Формализуем целевую функцию и ограничения суммарного объема предметов в следующем виде:

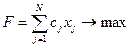. (4.48)

Ограничения на допустимый объем запишем так:

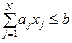; (4.49)

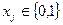. (4.50)

Таким образом, выражения (4.48) - (4.50) представляют собой ММ задачи о ранце. Для решения задач о ранце используют различные методы, имеющие разную трудоемкость, при этом иногда необходимо получить не оптимальное решение, а близкое к нему. Поэтому в этом случае используют эвристический метод. Алгоритм эвристического метода включает в себя следующие этапы:

1) Отсортировать все предметы по убыванию ценности , .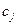

2) Загрузить в ранец самый ценный предмет.

3) Выбрать следующий j- й предмет и проверить ограничение на объем b ранца с учетом уже загруженных предметов.

4) Если ограничение выполнено, то загрузить j- й предмет в ранец, в противном случае этот предмет не загружать, а выбрать следующий по ценности (j+ 1)-й предмет с проверкой ограничения и т.д.

5) Выбрать следующий, менее ценный предмет и проверить ограничение. Далее – согласно п. 4 до тех пор, пока все предметы будут выбраны.

Задача о ранце может возникнуть при отправке грузового космического корабля на станцию, находящуюся на орбите. При этом появляется второй критерий – минимум суммарной массы предметов:

,

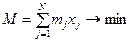где m_j – масса каждого предмета.

Пусть портфель заказов некоторой фирмы включает в себя n работ (проектов, заданий и т.п.). Каждая j -я работа требует для своего выполнения расхода ресурсов i -го вида в объеме 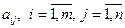. Известно, что каждая работа может принести фирме доход в размере 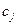единиц. Известно, что для выполнения работ в требуемый период (месяц, год) фирма располагает ресурсами в объемах 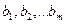. Если выполняются все условия вида:

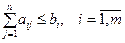, (4.51)

то фирма в планируемом периоде может выполнить все n работ и получить при этом прибыль 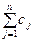. Если хотя бы одно из неравенств (4.51) не выполняется, то возникает задача оптимального выбора из портфеля заказов при ограничениях на имеющиеся ресурсы.

Выбор выполняемых работ будет произведен с помощью вектора 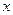, компоненты которого удовлетворяют условию (4.43). Условие достаточности для отобранных работ с учетом условия (4.43) записывается так:

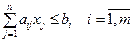. (4.52)

Суммарная прибыль от реализации всех отобранных работ определяется выражением вида:

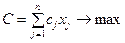. (4.53)

Совместно с требованиями максимума прибыли при отборе работ можно использовать целевую функцию, которая описывает суммарные затраты времени на выполнение всех отобранных работ:

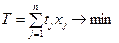. (4.54)

Таким образом, выражения (4.53), (4.54), (4.52), (4.43) описывают двухкритериальную, линейную, дискретную ММ оптимального выбора работ из портфеля заказов.

Пример. Пусть фирма к началу месяца получила заказы на разработку пяти комплексов программ (КП). В этом месяце (26 рабочих дней) фирма имеет фонд з/п 100 000 рублей и 8 свободных разработчиков, которые могут быть привлечены к выполнению поступивших заказов. Технико-экономические показатели каждого КП представлены в таблице:

№ КП Показатели
Прибыль (млн.р.)
з/п (тыс. рублей)
Требуемая численность (человек)
Время разработки (р.д.)

Здесь 1-й и 4-й показатели (прибыль и время разработки) являются критериями оптимизации, з/п и численность образуют ограничения.

Модель вида (4.53), (4.54), (4.52), (4.43) примет вид:

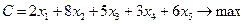; (4.53')

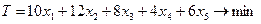; (4.54')

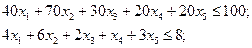(4.52')

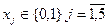. (4.43')

Пользуясь эвристическим алгоритмом, рассмотренном в задаче о ранце, решим однокритериальную задачу (4.53'), (4.52'), (4.43'):

Возьмем на разработку самый прибыльный комплекс программ – второй: х ₂ = 1. Ограничения (4.52') выполняются. Добавим 5-й КП – первое ограничение по з/п выполнилось, второе – не выполнилось (численность 6 + 3 = 9 превысила допустимое значение), следовательно, 5-й КП добавлять нельзя. Возьмем вместо него 3-й: х ₃ = 1 – оба ограничения выполнились, причем, что называется, под завязку: з/п 70 + 30 = 100; численность 6 + 2 = 8. Получили решение, при котором прибыль якобы максимальна:

С = 8 + 5 = 13 (млн. руб).

Однако существует решение данной задачи: х ₃ = 1, х ₄ = 1, х ₅ = 1, при котором и прибыль больше: С _max = 14 млн. руб, и з/п меньше – 70 тыс. руб., что меньше 100 000 руб, и для выполнения работы может быть занято 6 человек, а не 8. Этот результат подтверждает квазиоптимальность эвристического подхода к решению задач ПР.

1. Сформулируйте задачу оптимального выбора.

2. Приведите математическую модель задачи оптимального выбора в общем виде.

3. Сформулируйте задачу о ранце.

4. Приведите математическую модель задачи о ранце.

5. Приведите алгоритм эвристического метода при решении задачи о ранце.

6. Запишите критерий минимума суммарной массы предметов в ранце.

7. Сформулируйте задачуоптимального выбора выполняемых работ.

8. При каком условии фирма может выполнить все запланированные работы и получить при этом прибыль?

9. Приведите критерий суммарной прибыли от реализации всех отобранных работ.

10. Приведите критерий суммарных затрат времени на выполнение всех отобранных работ.

11. Приведите двухкритериальную ММ оптимального выбора работ из портфеля заказов.

Лекция 8

Все рассмотренные выше ММ, являются линейными детерминированными моделями. В данном разделе будут рассмотрены примеры нелинейных моделей. Нелинейные модели обычно строятся с помощью двух подходов:

1) Использование закономерностей формул фундаментальных и прикладных наук.

2) Путем непосредственного вывода входящих в модель воздействий.