Линейные модели задач принятия решений

КОНТРОЛЬНЫЕ ВОПРОСЫ 2

1. Дайте определение математической модели.

2. В каких случаях применяют ММ?

3. Перечислите требования, предъявляемые к ММ.

4. Сформулируйте задачу формирования оптимального решения.

5. Перечислите виды ММ.

6. Охарактеризуйте каждый из видов ММ.

7. Перечислите этапы формирования оптимальных решений.

8. Перечислите математические методы формирования оптимальных решений.

9. Охарактеризуйте каждый из методов формирования оптимальных решений.

10. В каком случае можно использовать аналитический метод Лагранжа?

11. Перечислите недостатки метода Лагранжа.

Данные модели занимают основное место в ТПР. Это объясняется тем, что линейные модели являются простыми и наглядными, линейные задачи решаются с помощью конечных численных методов. Отметим, что линейные модели вообще являются первым этапом решения практических задач за счёт их простоты. В этом случае при определённых предположениях нелинейные зависимости заменяются их линейными аппроксимациями. На рисунке 4.1 функция f (x) – исходная нелинейная зависимость, а 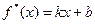– ее линейная аппроксимация. Такая замена правомерна только при выполнении условия .

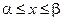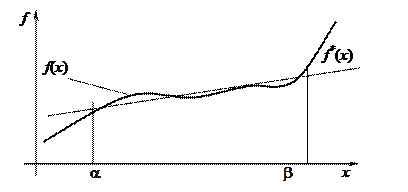
Рис. 4.1

Линейные модели в ТПР в основном строятся двумя путями:

· непосредственного вывода зависимости f^* (x);

· путём использования типовых моделей при конкретизации параметров применительно к решаемой задаче.

При использовании непрерывных линейных моделей 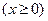используются методы решения задач линейного программирования (симплекс метод, метод обратной матрицы и так далее). При использовании дискретных линейных моделей применяются методы «отсечений» ветвей и границ, а также всевозможные эвристические методы. При построении линейных моделей в ограничениях следует избегать употребления строгих неравенств, так как в этом случае оптимального решения может не существовать.

Пример: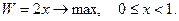

Оптимального решения этой задачи (рис. 4.2) не существует, так как переменная 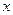принадлежит полуинтервалу [0,1), где 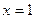не входит в множество допустимых решений даннойзадачи. Если ограничение заменить на 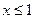, то множество допустимых значений х будет принадлежать интервалу 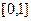и тогда ,
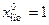а .

4.1. Задача выбора оптимальной производственной программы
предприятия

Рассмотрим классическую постановку. Пусть предприятие имеет возможности выпускать n видов продукции, располагая при этом m видами сырья. Запасы этих ресурсов (материальных, финансовых, временных, людских и т.п.) составляют соответственно 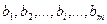единиц. Для каждого j -го вида продукции 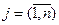считаются заданными 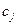– прибыль от реализации единицы продукции, 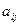– затраты i -го вида ресурсов на выпуск единицы продукции. Требуется найти оптимальное значение выпуска каждого вида продукции за определенный период (день, месяц и т.п.) в виде вектора решений 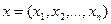, обеспечивающего предприятию максимальную прибыль (цель) при заданных ресурсах.

Математическую модель задачи будем строить путём непосредственного вывода входящих в неё зависимостей. Суммарное значение прибыли от реализации всей продукции опишем зависимостью вида

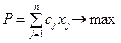. (4.1)

Ограничения на расход имеющихся ресурсов на предприятии запишутся как

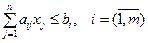, (4.2)

на выпускаемую продукцию накладываются ограничения

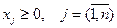. (4.3)

Задача линейного программирования решается известными численными методами, например методом Гомори и Симплекс-методом. При решении практических задач эта модель дополняется рядом критериев и ограничений.

Пусть известно, что на k- еизделие на рынке имеется фиксированный спрос в 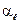. Это условие можно формализовать как:

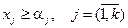. (4.4)

Будем считать, что по выпуску r изделий вида 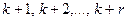предприятие имеет ограничение производительной мощности, позволяющее ему выпускать эту продукцию не более чем 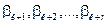. Этот факт можно описать ограничением вида:

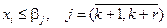. (4.5)

На остальную часть изделий реальные ограничения отсутствуют, поэтому их можно представить в виде

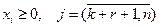. (4.6)

Таким образом, первое развитие класса задач (4.1) - (4.3) состоит в замене условия (4.3) на ограничения (4.3) - (4.6) при заданных значениях a и b.

Будем считать заданными значения трудоёмкости (затрат времени) 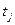на выпуск продукции j -го вида, 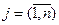, тогда общие затраты времени на выпуск запланированной продукции определяется по формуле вида:

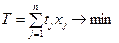. (4.7)

Величину (4.7) можно рассматривать как дополнительную целевую функцию. Если в задаче (4.1) - (4.3) критерий (4.1) заменить на критерий (4.7), то получим тривиальное решение 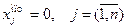. Поэтому с этой целевой функцией (4.7) необходимо использовать ограничение вида (4.4) - (4.6).

Кроме целевой функции (4.7) можно использовать целевую функцию вида:

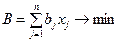, (4.8)

где 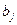– численность работников, участвующих в изготовлении единицы 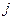-ой продукции.

Рассмотренные выше модели могут быть использованы при планировании производства изделий в больших количествах и с небольшой стоимостью, а так же «сыпучей» продукции (круп, цемент). Для использования в задачах при планировании производства уникальных изделий (самолеты, корабли и т.д.), обладающих значительной стоимостью, условия (4.3) должны быть заменены на целочисленные 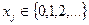, 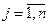. В этом случае получим дискретную линейную модель.