Вычисление поправок за центрировку и редукцию

Пусть на пункте с центром в точке О выполняются угловые измерения, теодолит находится в точке J, визирный цилиндр в точке V. Из точки J проведем направление J А = 0⁰ на начальный пункт А и направление J В на какой-либо другой пункт В; из точки V - направления V А и VВ на те же пункты. Обозначим М измеренные направления на пункте, отсчитывае­мые от начального. Пусть е, Θ - элементы центрировки, а е₁, Θ₁ - элементы редукции на пункте О. Проведем из точки О направление ОВ' параллельно направлению JВ. Угол с" = В'ОВ равен поправке за центрировку теодолита, которую необходимо ввести в измеренное направление JВ, чтобы получить искомое направление ОВ между центрами пунктов О и В. Углы с" при точках О и В равны. Решив треугольник JOB, в кото­ром s = О В- длина стороны между пунктами О и В, а угол ОJ В равен (М + Θ) - 360⁰, напишем .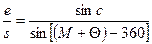

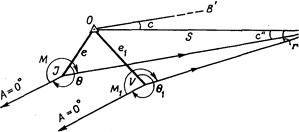
Так как угол с мал, формула для вычисления поправок в измеренные направления за центрировку теодолита будет иметь вид .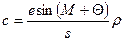

Поскольку визирная цель V находится не над центром пункта О, измеренное на пункте В направление BV следует исправить поправкой r = OBV за редукцию визирной цели V. Решив треугольник OBV, в котором s = ОВ, а угол OVB равен 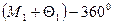, найдем малый угол r, т.е. поправку в направление BV за редукцию визирной цели .

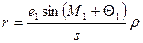Необходимо отметить, что поправки за центрировку теодо­лита вводят в направления, измеренные на пункте О, а по­правки за редукцию визирной цели со своим знаком в обрат­ные направления, т. е. в направления А V, BV,..., поскольку визирование с пунктов А, В,... производится не на центр пункта О, а на визирную цель V, не совпадающую с ним.

Поправки с и r в триангуляции и полигонометрии 1-2 клас­сов вычисляют с точностью до 0,001", а на пунктах 3 и 4 классов до 0,01".