2014-02-24
2835
Неинвариантность дифференциалов порядка выше первого
Рассмотрим дифференцируемую функцию n переменных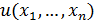 
. Вычислим ее первый дифференциал:
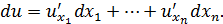
В правой части этого равенства стоит функция от переменных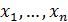 
, 
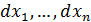- некоторые фиксированные постоянные. Возьмем дифференциал от левой и правой частей: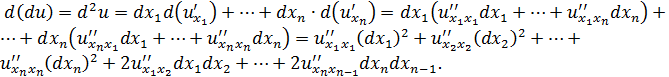
Формально можно записать:
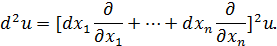
Аналогично,
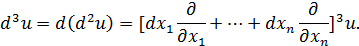
Вообще, справедлива формула:
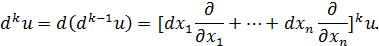
Рассмотрим функцию двух переменных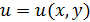 
. Запишем формулы первого, второго и третьего дифференциалов этой функции:
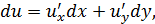
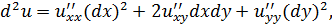
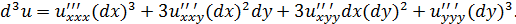
Исследуем, является ли дифференциал порядка выше первого инвариантной величиной. Пусть функция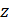 
является сложной функцией переменных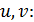 
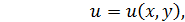x=x(u,v), y=y(u,v);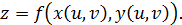 
Справедлива формула второго дифференциала:
(*)
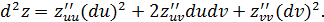Докажем, что нельзя записать, как это мы делали для первого дифференциала, что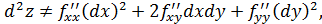
то есть форма второго дифференциала зависит от того, являются ли используемые переменные зависимыми или нет.
Имеем:
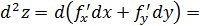{так как первый дифференциал инвариантен}=
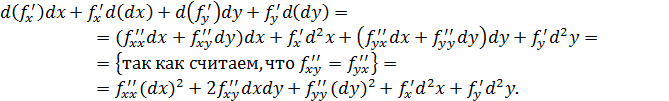
Если бы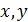 
были независимыми переменными, то была бы справедлива формула, аналогичная формуле (*). Но в нашем случае, когда 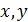являются в свою очередь некоторыми функциями, видим, что форма второго дифференциала меняется, появляются два новых слагаемых 
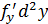. Видим, что форма второго дифференциала неинвариантна.
Однако, существует частный случай, когда можно говорить, что форма второго дифференциала инвариантна. Это случай линейной замены переменных:
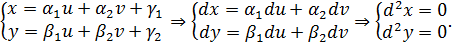
Отсюда в случае линейной замены переменных действительно получаем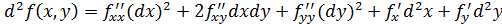
П.3. Геометрические приложения частных производных.
