Касательный вектор к кривой. Нормаль к поверхности.
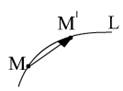
1) Касательный вектор. Рассмотрим кривую L в пространстве, заданную параметрическими уравнениями:
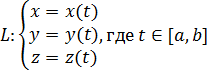
Фиксируем некоторое значение 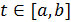 , тем самым фиксируем некоторую точку M на кривой L:
, тем самым фиксируем некоторую точку M на кривой L: 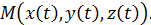 Придадим переменной t некоторое приращение
Придадим переменной t некоторое приращение 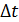 , получим точку
, получим точку 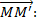
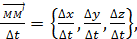
Пусть 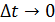 . Тогда из рисунка мы видим, что вектор
. Тогда из рисунка мы видим, что вектор 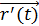 является касательным вектором к кривой L.
является касательным вектором к кривой L.
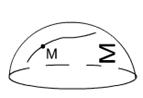 2) Касательная плоскость к поверхности
2) Касательная плоскость к поверхности 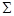 .
.
Пусть задана поверхность 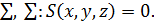
Пусть точка 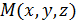 - произвольная точка на поверхности
- произвольная точка на поверхности 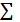 то есть ее координаты удовлетворяют уравнению поверхности
то есть ее координаты удовлетворяют уравнению поверхности 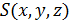 .
.
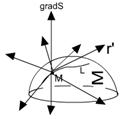
Проведем через точку M кривую L, целиком лежащую на поверхности 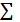 :
: 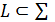 .
.
Строим 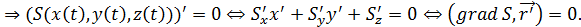
Здесь мы ввели вектор 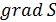 - градиент функции
- градиент функции 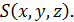
Вектор 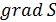 перпендикулярен касательному вектору ко кривой L в точке M.
перпендикулярен касательному вектору ко кривой L в точке M.
 Соотношение (
Соотношение (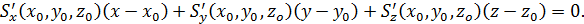
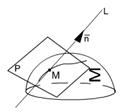 Рассмотрим L - нормаль к поверхности
Рассмотрим L - нормаль к поверхности 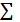 в точке
в точке 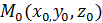 .Вектор
.Вектор 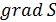 является направляющим вектором этой прямой, отсюда выписываем уравнение нормали к поверхности
является направляющим вектором этой прямой, отсюда выписываем уравнение нормали к поверхности 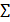 в точке
в точке 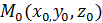 :
:
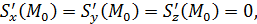 или хотя бы одна из частных производных не существует в этой точке, то касательная плоскость в точке
или хотя бы одна из частных производных не существует в этой точке, то касательная плоскость в точке 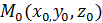 не существует.
не существует.
Рассмотрим геометрический смысл первого дифференциала. И спользуем результаты, полученные выше.
Рассмотрим функцию двух переменны 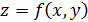 . Пусть точка
. Пусть точка 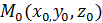 принадлежит области определения функции z. Тогда точка
принадлежит области определения функции z. Тогда точка 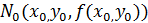 лежит на поверхности
лежит на поверхности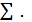 Фиксируем приращения
Фиксируем приращения 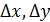 . Имеем:
. Имеем:
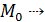
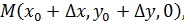
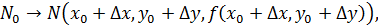
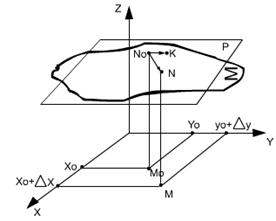
точка N лежит на поверхности, точка M лежит на плоскости, касающейся поверхности в точке 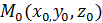 :
:
Пусть P касательная плоскость к поверхности 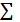 в точке
в точке 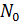
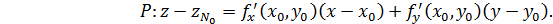
Пусть точка 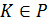 ,
, где координата
где координата 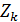 удовлетворяет уравнению плоскости P.
удовлетворяет уравнению плоскости P.
Имеем:
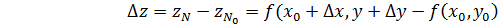
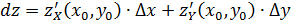
Отсюда получаем геометрический смысл первого дифференциала:
первый дифференциал 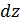 геометрически равен приращению аппликаты точки приращению аппликаты точки касательной плоскости, если переменным
геометрически равен приращению аппликаты точки приращению аппликаты точки касательной плоскости, если переменным 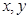
приданы приращения 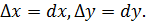
Если функция z дифференцируема в точке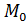 , то верно соотношение (точки K и N имеют совпадающие проекции на плоскость OXY)
, то верно соотношение (точки K и N имеют совпадающие проекции на плоскость OXY) 
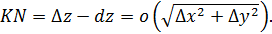
 2014-02-24
2014-02-24 3109
3109