Задача расчета режима сети, основные допущения
Расчет рабочих режимов разомкнутых и простых замкнутых электрических сетей
Основную задачу расчета режима сети составляет определение параметров режима. Как уже указывалось, к таким параметрам относятся: токи на участках сети, активные и реактивные мощности, напряжение в узлах сети, частота и др.
Исходными данными для расчета служат: расчетные мощности нагрузок, заданные величины напряжения в отдельных точках, схема электрических соединений сети, характеризующая взаимную связь ее элементов и другие величины.
Основным методом для электрического расчета сети является метод последовательных приближений (итераций), который предусматривает постепенный переход от более грубых ответов на поставленную задачу к более точным решениям. Первое приближение (нулевая итерация) при этом может быть получено на основании тех или иных представлений о возможных значениях искомых величин. Применительно к электрическим сетям в качестве первого приближения принимают равенство напряжений во всех точках сети номинальному напряжению. Это позволяет определить токи нагрузок и остальные параметры режима сети, в том числе и напряжения на зажимах нагрузки. Найденные напряжения являются уже вторым приближением к истинному решению. На основании этого можно снова найти токи и продолжать выполнять расчеты до тех пор, пока результаты последующих приближений не будут с заданной точностью отличаться от результатов предыдущих.
|
|
|
Практически при проведении расчетов электрических сетей можно ограничится второй и первой итерациями. К числу таких расчетов относятся расчеты сетей 35 кВ и ниже, а в ряде случаев – проектные расчеты сетей напряжением 110 и 220 кВ. При анализе режимов сетей 35 кВ и ниже ограничиваются первым приближением. Связано это с тем, что требования потребителей к качеству напряжения определяет необходимость обеспечивать для всех точек таких сетей напряжения, мало отличающихся от номинальных, которые принимаются при расчетах первого приближения. Получаемая при этом ошибка лежит в пределах точности расчета. Ошибка, получаемая при ограничении расчетов сетей 110 и 220 кВ вторым приближением, также оказывается в пределах точности расчета.
Рассмотрим простейшую линию трехфазного тока с симметричной нагрузкой на конце (см.рисунок 4.1).

Рисунок 4.1
Нагрузка задана либо током I и cosj при фазном напряжении U на конце линии, либо мощностью S = P + jQ.
на конце линии, либо мощностью S = P + jQ.
Расчет проводится с помощью векторной диаграммы токов и напряжений для одной фазы линии, что допускается, так как нагрузка во всех фазах симметрична.
|
|
|
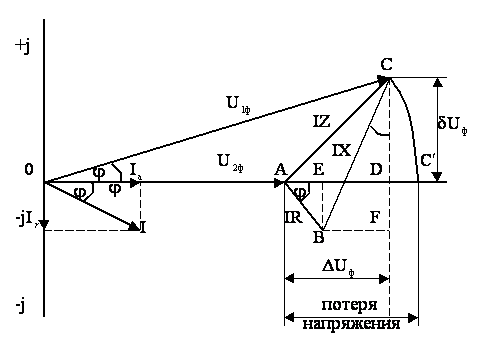
Рисунок 4.2 - Векторная диаграмма линии с нагрузкой на конце
Известны ток нагрузки I, cosj и напряжение U . Необходимо определить U
. Необходимо определить U . По действительной оси откладываем вектор заданного напряжения в конце линии U
. По действительной оси откладываем вектор заданного напряжения в конце линии U (ОА). Из начала координат откладываем вектор тока I под углом j. Его активная составляющая направлена по действительной оси I
(ОА). Из начала координат откладываем вектор тока I под углом j. Его активная составляющая направлена по действительной оси I , а реактивная составляющая -jI
, а реактивная составляющая -jI - по мнимой оси в отрицательном направлении. Таким образом, при принятом расположении вектора напряжения и тока на векторной диаграмме знак минус у мнимой части комплекса тока характеризует индуктивный (отстающий) ток нагрузки потребителя.
- по мнимой оси в отрицательном направлении. Таким образом, при принятом расположении вектора напряжения и тока на векторной диаграмме знак минус у мнимой части комплекса тока характеризует индуктивный (отстающий) ток нагрузки потребителя.
Далее из точки А откладываем параллельно вектору тока I вектор падения напряжения в активном сопротивлении линии IR (АВ) и под углом 90 к нему в сторону опережения – вектор падения напряжения в реактивном сопротивлении IX (ВС). Соединив точку А с точкой С, получим вектор полного па-
к нему в сторону опережения – вектор падения напряжения в реактивном сопротивлении IX (ВС). Соединив точку А с точкой С, получим вектор полного па-
дения напряжения в рассматриваемой линии IZ (АС). Чтобы найти напряжение U , соединим точку С с началом координат, получаем вектор фазного напряжения в начале линии U
, соединим точку С с началом координат, получаем вектор фазного напряжения в начале линии U (ОС).
(ОС).
Падение напряжения в линии
IZ = 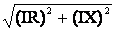
может быть разложено на составляющие:
а) продольную DU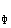 = АD
= АD
б) поперечную d U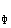 = DC
= DC
т.е. IZ = DU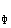 + jd U
+ jd U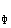 .
.
Определим эти составляющие. Для этого опустим перпендикуляры из точек В и С на действительную и мнимую оси. В результате получим отрезки:
АЕ = IRcosj; ED = BF = IXsinj;
CF = IXcosj; BE = DF = IRsinj.
Отсюда продольная составляющая
DU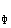 = AD = AE + ED = IRcosj + IXsinj = I
= AD = AE + ED = IRcosj + IXsinj = I R + I
R + I X, (4.1)
X, (4.1)
d U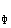 = DC = CF - DF = IXcosj - IRsinj = I
= DC = CF - DF = IXcosj - IRsinj = I X + I
X + I R. (4.2)
R. (4.2)
Напряжение в начале линии
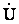
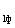 = U
= U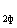 + DU
+ DU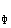 + jdU
+ jdU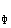 ,
,
а модуль напряжения
U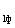 =
= 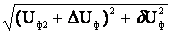 . (4.3)
. (4.3)
В результате построения диаграммы выше был получен вектор полного падения напряжения в линии. Следует отметить, что под падением напряжения понимают геометрическую разность потенциалов между началом и концом линии.
При расчете сетей 35 кВ и ниже обычно вводятся упрощения, заключающиеся в том, что напряжение в начале линии определяют не по падению напряжения, а по потере напряжения. Под потерей напряжения понимают алгебраическую разность абсолютных значений напряжений в начале и в конце линии.
Для определения потери напряжения на диаграмме совместим отрезок ОС с осью действительных величин (отрезок О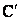 ).
).
Отрезок А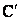 = О
= О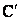 - ОА = U
- ОА = U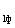 - U
- U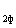 представляет собой потерю напряжения.
представляет собой потерю напряжения.
Так как для сетей 35 кВ и ниже углы между U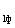 и U
и U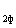 очень малы, а значит мал и отрезок D
очень малы, а значит мал и отрезок D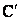 , то можно считать, что потеря напряжения приблизительно равна продольной составляющей падения напряжения
, то можно считать, что потеря напряжения приблизительно равна продольной составляющей падения напряжения
АD» A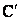 » DU
» DU » IRcosj + IXsinj. (4.4)
» IRcosj + IXsinj. (4.4)
Потеря линейного напряжения
DU = 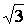 DU
DU =
= 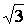 I(Rcosj + Xsinj). (4.5)
I(Rcosj + Xsinj). (4.5)
Векторная диаграмма линейных напряжений будет выглядеть аналогично диаграмме фазных напряжений.
При задании нагрузки активной и реактивной мощностью Р+jQ величина потери напряжения определяется следующим образом
Так как I = Icosj =
= Icosj = 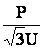 и I
и I = Isinj =
= Isinj =  , то, подставив эти значения в (4.5), получим
, то, подставив эти значения в (4.5), получим
DU = 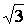 (IRcosj + IXsinj) =
(IRcosj + IXsinj) = 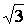
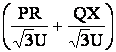 ,
,
или
DU = 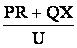 . (4.6)
. (4.6)
Часто при расчетах напряжение у потребителей бывает неизвестно, то вместо действительного в конце линии можно принимать номинальное напряжение
DU = 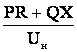 . (4.7)
. (4.7)
При расчетах сети с несколькими нагрузками величина потери напряжения определяется как сумма потерь напряжений на всех участках сети
DU = 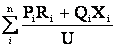 . (4.8)
. (4.8)
 2014-02-24
2014-02-24 2598
2598
