Пусть имеется ДСК в пр-ве
и произвольный в-р 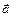
(б. считать, что его начало
совпадает с началом координат).
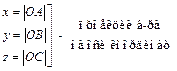
Из рисунка имеем:
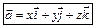
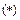
Т.о. док-но:
если в пр-ве задан дек. базис, то любой в-р м.б. представлен в виде суммы  , где
, где 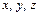 – прекции в-ра на координатные оси. Ф-ла
– прекции в-ра на координатные оси. Ф-ла  наз-ся разложением
наз-ся разложением
в-ра по базису 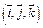 , числа
, числа 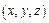 – координаты в-ра
– координаты в-ра 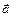 в данном базисе.
в данном базисе.
Замечание. На плоскости
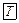 О соответствии мд. в-рами и их коорд-ми при линейных операциях
О соответствии мд. в-рами и их коорд-ми при линейных операциях
Линейные операции над в-рами сводятся к таким же операциям над их одноименными координатами:
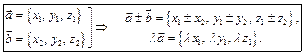
Д-во. Пусть 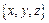 – координаты в-ра
– координаты в-ра 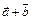 в данном базисе. Тогда
в данном базисе. Тогда 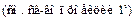
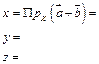
Остальное (-,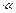 ) аналогично.
) аналогично.
В частности,  .
.
Правило «конец - начало»
Радиус-вектором точки 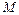 называется вектор, идущий из начала координат в данную точку: называется вектор, идущий из начала координат в данную точку:
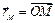 .
Координаты точки – координаты ее радиус-вектора. .
Координаты точки – координаты ее радиус-вектора.
|
Справедливо утверждение
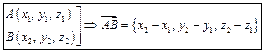 .
.
Д-во.
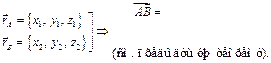
 2014-02-09
2014-02-09 952
952








