Основные понятия. СЛАУ называется система вида

СЛАУ называется система вида

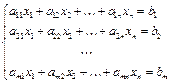(4)

где числа 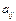– коэффициенты системы, 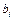– свободные члены, 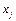– неизвестные (подлежат нахождению).

Решением системы (4) называется 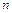значений неизвестных , _____________________________________________________

____________________________________________________________________

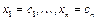Известно, что СЛАУ может

-не иметь решений;

-иметь единственное решение (единственный набор);

-иметь бесконечное множество решений.

В 1-м случае с-ма называется несовместной, во 2-м – определенной, в 3-м – неопределенной.

Решить систему –________________________________________

_______________________________________________________________

Две системы называются эквивалентными, если они имеют одинаковый набор решений. Эквивалентные системы получаются, в частности, при элементарных преобразованиях над уравнениями системы ().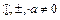

Систему (4) можно записать в виде

.

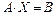Здесь 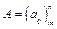- основная матрица системы,

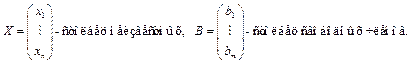
Матрица 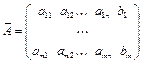называется расширенной матрицей системы.

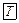Кронекера-Капелли

СЛАУ совместна тогда и только тогда, когда

.

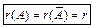Если при этом

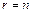– система имеет единственное решение,

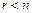– система имеет бесконечное множество решений (без доказательства).