Расчет неразветвленной магнитной цепи постоянного тока

Формула, выражающая закон полного тока магнитной цепи, была получена для кольцевого магнитопровода постоянного поперечного сечения и с равномерно распределенной обмоткой. Эту формулу распространяют и на магнитные цепи, где намагничивающая обмотка сосредоточена на ограниченном участке магнитопровода, а отдельные участки цепи выполнены из различных ферромагнитных и неферромагнитных материалов и имеют различное поперечное сечение.

В приближенных расчетах магнитных цепей принимают, что магнитный поток на всех участках цепи остается одним и тем же, хотя на самом деле в магнитной цепи образуются также потоки рассеяния Ф_р, которые замыкаются по воздуху, а не следуют по пути магнитопровода.

В расчетах магнитных цепей различают прямую и обратную задачи.

1. Прямая задача

Задано: 1) геометрические размеры магнитной цепи; 2) характеристика B = f(H) (кривая намагничивания) ферромагнитных материалов, из которых выполнена магнитная цепь; 3) магнитный поток Ф, который надо создать в магнитной цепи.

Требуется найти намагничивающую силу обмотки F = IW.

Решение задачи рассматривается применительно к магнитопроводу, представленному на рисунке.

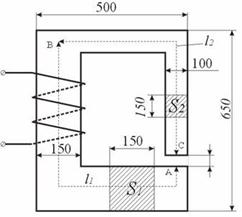
Рис. 10. Магнитная цепь

1. Магнитная цепь разбивается на ряд участков с одинаковым поперечным сечением S, выполненном из однородного материала.

2. Намечается путь прохождения средней магнитной линии (на рис. показано пунктиром).

3. Т.к. магнитный поток на всех участках цепи остается постоянным, то магнитная индукция B = Ф / S на каждом из участков и напряженность магнитного поля Н неизменны. Это позволяет сравнительно просто определить значение 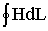для контура, образованного средней магнитной линией, а следовательно, найти искомую величину намагничивающей силы, поскольку .

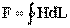Запишем интеграл 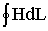в виде суммы интегралов с границами интегрирования, совпадающими с началом и концом каждого участка цепи. Тогда

.

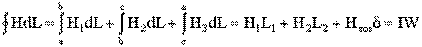где: L₁ и L₂ – длины ферромагнитных участков цепи [м].
d – ширина воздушного зазора, [м].

4. Значения Н₁ и Н₂ определяют по известным величинам магнитной индукции В с помощью кривых намагничивания, соответствующих ферромагнитных материалов.

А для воздушного зазора

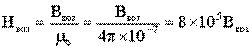А/м.

Разделим каждое слагаемое на магнитный поток Ф, получим:

(*)

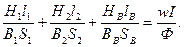Обозначим:

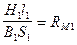- магнитное сопротивление участка 1;

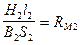- магнитное сопротивление участка 2;

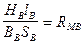- магнитное сопротивление воздушного зазора.

С учетом обозначений перепишем выражение (*):

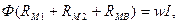
или

(**)

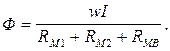Последнее выражение, т.е. зависимость магнитного потока от магнитодвижущей силы (wI) и магнитных сопротивлений участков магнитной цепи называют основным законом магнитной цепи.

Заметна аналогия между уравнением (**) и законом Ома для полной цепи:

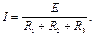
Составим таблицу аналогий соответствующих величин.

Таблица

Магнитные величины	Электрические величины
Наименование	Обозначение	Ед. измерения	Наименование	Обозначение	Ед. измерения
Магнитный поток	Ф	Вб	Сила тока	I	A
Магнитодвижущая сила	wI	A	Электродвижущая сила	Е	В
Магнитное сопротивление	RM		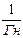Электрическое сопротивление	R	Ом
Магнитное напряжение	UM=RMФ =H l	А	Электрическое напряжение	U=RI	B

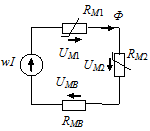
Пользуясь аналогиями, можно изобразить схему замещения магнитной цепи, изображенной ранее, в виде. Полученная цепь содержит последовательно соединенные нелинейные элементы R_{M 1} и R_{M 2}. Их нелинейность обусловлена зависимостью от напряженности магнитного поля Н или от силы тока в обмотке I, т.е. от МДС действующей в контуре.

2. Обратная задача

Задано:

1. Геометрические размеры магнитной цепи;
2. Характеристики ферромагнитных материалов;
3. Намагничивающая сила обмотки F.

Требуется определить магнитный поток Ф.

Непосредственное использование формулы 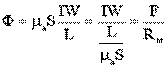для определения магнитного потока Ф оказывается невозможным, поскольку магнитное сопротивление цепи переменное и само зависит от величины магнитного потока. Такие задачи решаются методом последовательного приближения в следующем порядке. Задаются рядом произвольных значений магнитного потока в цепи и для каждого из этих значений определяют необходимую намагничивающую силу обмотки так, как это делается при решении прямой задачи.

По полученным данным строят кривую Ф(F) – вебер-амперную характеристику. Имея эту зависимость, нетрудно для заданного значения намагничивающей силы найти величину магнитного потока.

Для оценки необходимого значения Ф можно пренебречь сопротивлением ферромагнитного участка и посчитать поток, который получится под действием намагничивающей силы F при сопротивлении воздушного участка. Это значение Ф заведомо больше расчетного.

Остальные значения можно давать меньше.

.

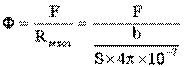Магнитные цепи электротехнических устройств переменного тока

Рассмотрим электромагнитное состояние устройства, состоящего из магнитопровода и намагничивающей обмотки, подключенной к источнику синусоидального напряжения.

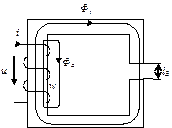
Под действием приложенного напряжения u возникает ток i, возбуждающий переменный магнитный поток Ф_t. При упрощенном анализе будем пренебрегать полями рассеяния Ф_d.

Поток Ф_t наводит в витках обмотки ЭДС самоиндукции 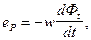условно-положительное направление которой выбирают одинаковым с направлением тока i в обмотке. Учитывая, что обмотка обладает электрическим сопротивлением R_К для схемы замещения дросселя, показанной на рисунке, можно записать уравнение электрического состояния:

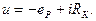
Пренебрегая сопротивлением обмотки (R_К =0), можно записать:

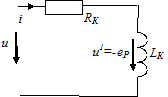
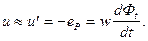
Предположим, что входное напряжение изменяется по закону 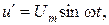можно записать:

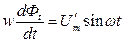или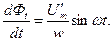

Решая последнее уравнение можно определить закон изменения магнитного потока:

,

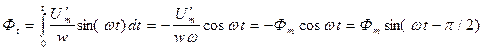где

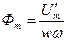есть амплитудное значение магнитного потока.

Из него следует, что амплитуда магнитного потока определяется только частотой w и амплитудой приложенного напряжения U_m, а также числом витков обмотки w. И амплитуда магнитного потока не зависит от вида и характеристик В (Н) магнитопровода и величины намагничивающего тока i.

Изобразим значения Ф_t, u¹ и е_Р в виде векторов на векторной диаграмме:

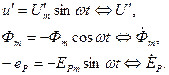
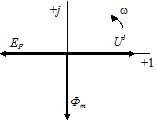
Отметим, что вектор потока Ф_m на 90° отстает от вектора напряжения U¹.

Таким образом, если к обмотке идеализированной индуктивной катушки с магнитопроводом подвести синусоидальное напряжение, то в магнитной цепи возникнет магнитный поток, изменяющийся также по синусоидальному закону, но отстающий от напряжения на угол 90 °.