Каждуй проводник с током создает в окружающем пространстве магнитное поле. Электрический ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле. В результате обобщения опытных данных был установлен закон, определяющий поле 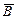 точечного заряда
точечного заряда 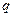 , свободно движущегося (т.е. с постоянной скоростью
, свободно движущегося (т.е. с постоянной скоростью 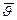 ):
):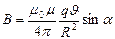 , где
, где 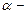 угол между
угол между 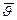 и радиус-вектором
и радиус-вектором 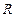 , проведенным от заряда к точке наблюдения. Получаем, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока:
, проведенным от заряда к точке наблюдения. Получаем, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока: 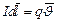 .
.
Данные закономерности справедливы лишь при малых скоростях 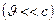 движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т.е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени расположен движущийся заряд.
движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т.е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени расположен движущийся заряд.
Из закона Ампера легко получить одно из фундаментальных физических соотношений: выражение для силы, действующей на движущуюся в магнитном поле заряженную частицу, - силы Лоренца. Пусти частицы с зарядом 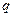 каждая движутся со скоростью
каждая движутся со скоростью 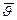 внутри провода сечением
внутри провода сечением 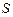 и длиной
и длиной 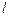 . Если
. Если 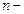 число свободных электронов в единице объема проводника (концентрация частиц), то сила тока
число свободных электронов в единице объема проводника (концентрация частиц), то сила тока 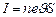 .
.
Сила Ампера 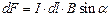 Для однородного прямолинейного проводника
Для однородного прямолинейного проводника 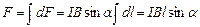 . С учетом того, что
. С учетом того, что 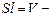 объем проводника, а
объем проводника, а 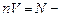 общее число зарядов, создающих ток, то
общее число зарядов, создающих ток, то 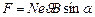
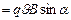 .
.
 Сила
Сила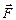 (сила Лоренца), действующая на заряд
(сила Лоренца), действующая на заряд 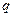 , движущийся со скоростью
, движущийся со скоростью 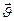 в магнитном поле с индукцией
в магнитном поле с индукцией 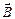 :
: 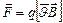 или
или 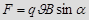 , где
, где 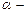 угол, образованный вектором скорости
угол, образованный вектором скорости 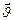 движения частицы и вектором
движения частицы и вектором 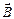 индукции магнитного поля.
индукции магнитного поля.

Впервые это выражение вывел нидерландский физик Хендрик Антон Лоренц. Формула замечательна тем, что ее нельзя объяснить без введения принципиально нового, невещественного объекта – поля. Ведь любая упругая среда передает возмущения от источника (магнита) к приемнику (заряженной частице) радиально. И действующая на приемник сила не может быть направлена столь странным для механики образом. Сила Лоренца направлена перпендикулярно векторам индукции магнитного поля и скорости частицы. В поле магнита, поднесенного к электронно-лучевой трубке, поток электронов смещается вниз.
Сила Лоренца изменяет только направление скорости, не изменяя ее модуля, т.е. работы не совершает и кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется.
Задача 4. Электрон, ускоренный разностью потенциалов 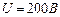 , движется параллельно прямолинейному длинному проводу на расстоянии
, движется параллельно прямолинейному длинному проводу на расстоянии 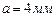 от него. Какая сила действует на электрон, если по проводнику пустить ток
от него. Какая сила действует на электрон, если по проводнику пустить ток 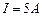 ?
?
|
Дано: Решение:
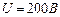
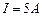
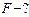 ,
,
Индукция магнитного поля проводника с током равна 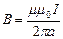 , получаем
, получаем 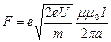 .
.
Ответ:
Задача 5. Электрон, ускоренный разностью потенциалов 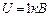 , влетел в однородное магнитное поле с индукцией
, влетел в однородное магнитное поле с индукцией 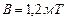 перпендикулярно к направлению линий поля. Определить радиус R, период вращения Т и момент импульса электрона.
перпендикулярно к направлению линий поля. Определить радиус R, период вращения Т и момент импульса электрона.
|
Дано: Решение:
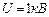
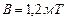
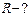 ,
, 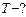 ,
,
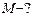
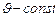 . Из механики известно, что постоянная сила, перпендикулярная к скорости, вызывает движение по окружности. Ускорение
. Из механики известно, что постоянная сила, перпендикулярная к скорости, вызывает движение по окружности. Ускорение 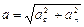 , где
, где 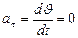 ,
, 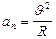 . Электрон будет двигаться с постоянным по модулю ускорением
. Электрон будет двигаться с постоянным по модулю ускорением 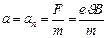 которое перпендикулярно скорости. Радиус кривизны траектории
которое перпендикулярно скорости. Радиус кривизны траектории 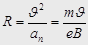 . Период обращения электрона не зависит от скорости:
. Период обращения электрона не зависит от скорости: 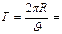
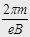 , Момент импульса электрона
, Момент импульса электрона  , но т.к. векторы
, но т.к. векторы 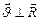 , то
, то 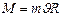 .
.
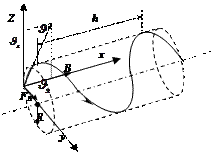
Задача 6. Электрон, обладающий скоростью 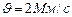 ., влетел в однородное магнитное поле с индукцией
., влетел в однородное магнитное поле с индукцией 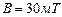 под углом
под углом 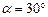 к направлению линий поля. Определить радиус R, период вращения Т и шаг h винтовой линии, по которой будет двигаться электрон.
к направлению линий поля. Определить радиус R, период вращения Т и шаг h винтовой линии, по которой будет двигаться электрон.
|
Дано: Решение:

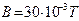
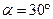
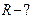 ,
, 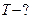 ,
,
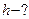
будет двигаться и вдоль поля со скоростью 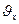 :
: 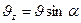 ,
, 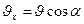 . В результате одновременного движения по окружности и по прямой электрон будет двигаться по винтовой линии. Т.к. сила Лоренца вызывает движение по окружности, то она является центростремительной силой
. В результате одновременного движения по окружности и по прямой электрон будет двигаться по винтовой линии. Т.к. сила Лоренца вызывает движение по окружности, то она является центростремительной силой 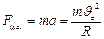
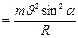 . Отсюда получаем
. Отсюда получаем 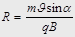 ,
, 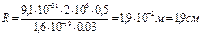 . Период обращения электрона
. Период обращения электрона 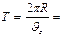
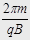 ,
, 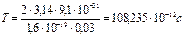 т.о. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду
т.о. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду 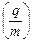 и магнитной индукцией поля, но не зависит от ее скорости (при
и магнитной индукцией поля, но не зависит от ее скорости (при 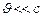 ). Шаг винтовой линии будет равен пути, пройденному электроном вдоль поля со скоростью
). Шаг винтовой линии будет равен пути, пройденному электроном вдоль поля со скоростью 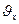 за время, которое понадобится электрону для того, чтобы совершить один оборот:
за время, которое понадобится электрону для того, чтобы совершить один оборот: 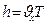
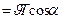 .
. 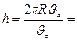
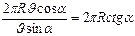
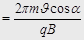 .
. 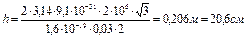
Ответ: 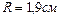 ,
, 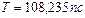 ,
, 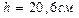 .
.
Если на движущийся электрический заряд помимо магнитного поля с индукцией 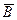 действует и электрическое поле с напряженностью
действует и электрическое поле с напряженностью 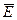 , то результирующая сила
, то результирующая сила 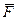 , приложенная к заряду, равна векторной сумме сил:
, приложенная к заряду, равна векторной сумме сил: 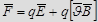 - формула Ленца.
- формула Ленца.
Разность потенциалов 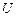 на концах проводника длиной
на концах проводника длиной 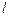 , движущегося в однородном магнитном поле со скоростью
, движущегося в однородном магнитном поле со скоростью 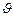 :
: 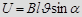 , где
, где 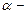 угол между направлением вектора скорости и вектора магнитной индукции.
угол между направлением вектора скорости и вектора магнитной индукции.
Эффект Холла: возникновение в металле (или полупроводнике) с током плотностью 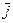 , помещенном в магнитное поле
, помещенном в магнитное поле 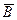 , электрического поля в направлении, перпендикулярном
, электрического поля в направлении, перпендикулярном 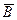 и
и 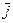 .
.

Это явление было обнаружено Холлом в 1879 г. и называется эффектом Холла или гальваномагнитнымявлением. Поместим металлическую пластину с током плотностью 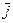 в магнитное поле
в магнитное поле 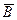 , перпендикулярное
, перпендикулярное 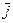 . Скорость носителей тока – электронов – направлена противоположно
. Скорость носителей тока – электронов – направлена противоположно 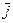 . Электроны испытывают действие силы Лоренца, которая направлена в данном случае вверх. У верхнего края пластинки возникнет повышенная концентрация электронов, а у нижнего – их недостаток. В результате между краями пластинки возникнет дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность
. Электроны испытывают действие силы Лоренца, которая направлена в данном случае вверх. У верхнего края пластинки возникнет повышенная концентрация электронов, а у нижнего – их недостаток. В результате между краями пластинки возникнет дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность 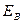 этого поперечного поля достигнет такой величины, что его действие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Тогда
этого поперечного поля достигнет такой величины, что его действие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Тогда 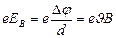 или
или 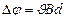 , где
, где 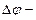 поперечная (холловская) разность потенциалов,
поперечная (холловская) разность потенциалов, 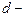 ширина пластинки. Т.к.
ширина пластинки. Т.к. 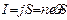 и
и 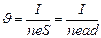 , т.е.
, т.е. 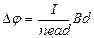
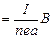 . Получаем, что поперечная разность потенциалов
. Получаем, что поперечная разность потенциалов 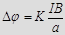 , где
, где 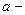 толщина пластины,
толщина пластины, 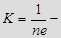 постоянная Холла, зависящая от вещества. Зная постоянную Холла и удельную проводимость материала
постоянная Холла, зависящая от вещества. Зная постоянную Холла и удельную проводимость материала 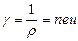 , можно найти подвижность носителей тока
, можно найти подвижность носителей тока 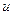 , определить концентрацию носителей тока, судить о природе проводимости полупроводников, т.к. знак постоянной Холла совпадает со знаком заряда носителей тока. Эффект Холла – наиболее эффективный метод изучения энергетического спектра носителей тока в металлах и полупроводниках. Он применяется так же для умножения постоянных токов в аналоговых вычислительных машинах, в измерительной технике (датчики Холла) и т.д.
, определить концентрацию носителей тока, судить о природе проводимости полупроводников, т.к. знак постоянной Холла совпадает со знаком заряда носителей тока. Эффект Холла – наиболее эффективный метод изучения энергетического спектра носителей тока в металлах и полупроводниках. Он применяется так же для умножения постоянных токов в аналоговых вычислительных машинах, в измерительной технике (датчики Холла) и т.д.
Закон полного тока.
Аналогично циркуляции вектора напряженности электростатического поля введем циркуляцию вектора магнитной индукции. Циркуляция вектора 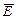 электростатического поля всегда равна нулю – электростатическое поле является потенциальным. Циркуляция вектора
электростатического поля всегда равна нулю – электростатическое поле является потенциальным. Циркуляция вектора 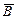 магнитного поля не равна нулю – вихревое поле, и зависит от выбора контура.
магнитного поля не равна нулю – вихревое поле, и зависит от выбора контура.
Рассмотрим магнитное поле бесконечного прямолинейного проводника с током 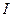 , находящегося в вакууме (см.рис.). Линии магнитной индукции представляют собой окружности, плоскости которых перпендикулярны проводнику, а центры лежат на его оси. Найдем циркуляцию вектора
, находящегося в вакууме (см.рис.). Линии магнитной индукции представляют собой окружности, плоскости которых перпендикулярны проводнику, а центры лежат на его оси. Найдем циркуляцию вектора 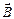 вдоль произвольной линии магнитной индукции – окружности радиуса
вдоль произвольной линии магнитной индукции – окружности радиуса 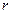 .
.

Опр. Циркуляцией вектора 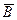 по заданному замкнутому контуру называется интеграл
по заданному замкнутому контуру называется интеграл 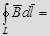
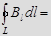
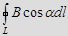 , где
, где 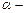 угол между
угол между 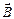 и
и  . Во всех точках линии индукции вектор
. Во всех точках линии индукции вектор 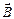 равен по модулю
равен по модулю 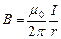 и направлен по касательной к этой линии, т.е.
и направлен по касательной к этой линии, т.е. 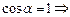
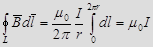 .
.
Получаем, что циркуляция вектора 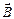 поля прямолинейного тока в вакууме одинакова вдоль всех линий магнитной индукции.
поля прямолинейного тока в вакууме одинакова вдоль всех линий магнитной индукции.
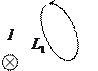 Данная формула справедлива для замкнутого контура произвольной формы, охватывающего бесконечно длинный проводник с током
Данная формула справедлива для замкнутого контура произвольной формы, охватывающего бесконечно длинный проводник с током 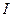 . Доказать!
. Доказать!
Циркуляция вектора магнитной индукции поля прямолинейного проводника с током вдоль замкнутого контура, не охватывающего этот проводник, равна нулю. 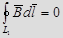 Доказать!
Доказать!
Соотношения (1) и (2) в вакууме универсальны. Они справедливы для магнитного поля проводника с током любой формы и размеров, а не только для поля бесконечного прямолинейного проводника с током. Доказать!
|
В общем случае магнитное поле может создавать целая система из 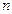 проводников с токами
проводников с токами 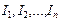 . Обозначим
. Обозначим 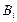 индукцию магнитного поля в вакууме одного
индукцию магнитного поля в вакууме одного 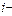 го проводника с током
го проводника с током 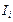 . Индукция результирующего магнитного поля, согласно принципу суперпозиции,
. Индукция результирующего магнитного поля, согласно принципу суперпозиции, 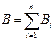 . Циркуляция вектора
. Циркуляция вектора  вдоль произвольного замкнутого контура
вдоль произвольного замкнутого контура 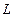 , проведенного в поле, равна
, проведенного в поле, равна 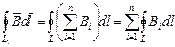 . Исходя из формул (1) и(2) получим:
. Исходя из формул (1) и(2) получим: 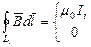 , следовательно,
, следовательно, 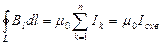 . В сумму входят только те токи, которые охватываются контуром
. В сумму входят только те токи, которые охватываются контуром 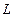 .
.

Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора 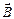 ):
): 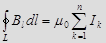 , где
, где 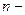 число проводников с токами, охватываемых контуром
число проводников с токами, охватываемых контуром 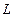 произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Закон справедлив только для поля в вакууме, т.к. для поля в веществе необходимо учитывать молекулярные токи.
произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Закон справедлив только для поля в вакууме, т.к. для поля в веществе необходимо учитывать молекулярные токи.
Напр., для системы токов, изображенной на рисунке: 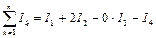 .
.
Теорема о циркуляции позволяет находить индукцию поля без применения закона Био – Савара – Лапласа.
Циркуляция вектора напряженности Н магнитного поля вдоль замкнутого контура, охватывающего ток I: 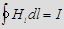 , где
, где 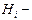 проекция вектора напряженности Н на направление касательной к контуру, содержащей элемент
проекция вектора напряженности Н на направление касательной к контуру, содержащей элемент 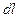 . Если контур охватывает n токов:
. Если контур охватывает n токов: 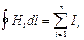 , где сумма – алгебраическая сумма токов, охватываемых контуром.
, где сумма – алгебраическая сумма токов, охватываемых контуром.
Замечание. Применение теоремы о циркуляции вектора магнитной индукции значительно упрощает расчеты симметричных магнитных полей. При этом важно, чтобы через точку, в которой требуется определить вектор 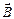 , можно было провести такой замкнутый контур
, можно было провести такой замкнутый контур 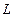 , совпадающий с линией индукции поля, для всех точек которого выполнялось соотношение
, совпадающий с линией индукции поля, для всех точек которого выполнялось соотношение 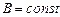 . В этом случае для всех элементов контура
. В этом случае для всех элементов контура 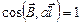 и уравнение приобретает простой вид:
и уравнение приобретает простой вид: 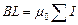 .
.
Магнитное поле соленоида и тороида.
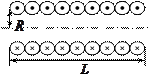
Соленоид – цилиндрическая катушка, состоящая из большого числа витков проволоки, образующих винтовую линию. Если витки расположены вплотную или очень близко друг к другу, то соленоид можно рассматривать как систему последовательно соединенных круговых токов одинакового радиуса с общей осью.
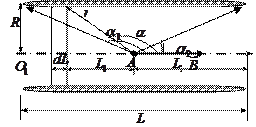
На рис. показано сечение соленоида радиуса 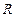 и длины
и длины 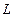 с током
с током 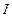 . Число витков соленоида
. Число витков соленоида 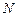 . Экспериментальное изучение магнитного поля соленоида показывает, что внутри соленоида поле является однородным, вне соленоида – неоднородным и очень слабым. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.
. Экспериментальное изучение магнитного поля соленоида показывает, что внутри соленоида поле является однородным, вне соленоида – неоднородным и очень слабым. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.
Магнитная индукция поля соленоида равна геометрической сумме магнитных индукций  полей всех витков этого соленоида. В произвольной точке А, лежащей на оси соленоида
полей всех витков этого соленоида. В произвольной точке А, лежащей на оси соленоида 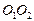 , все векторы
, все векторы  и результирующий вектор
и результирующий вектор  направлены по оси
направлены по оси 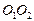 в ту сторону, куда перемещается буравчик с правой резьбой при вращении его рукояти в направлении электрического тока в витках соленоида. На малый участок соленоида длиной
в ту сторону, куда перемещается буравчик с правой резьбой при вращении его рукояти в направлении электрического тока в витках соленоида. На малый участок соленоида длиной 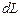 вдоль оси приходится
вдоль оси приходится 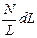 витков. Если
витков. Если 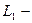 расстояние вдоль оси от этих витков до точки А, то магнитная индукция поля этих витков
расстояние вдоль оси от этих витков до точки А, то магнитная индукция поля этих витков 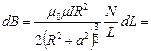
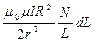 , т.к.
, т.к. 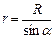 ,
, 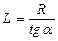 , то
, то 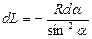 и
и 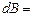
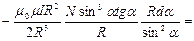
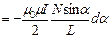 . В пределах соленоида угол
. В пределах соленоида угол 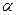 изменяется от
изменяется от 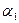 до
до 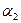 , поэтому
, поэтому 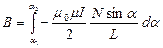
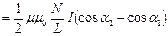 , где
, где 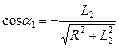 ,
,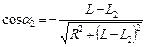 . В максимально, если
. В максимально, если 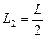 .
.
Магнитное поле длинного соленоида 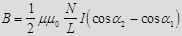 , где
, где 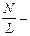 число витков на единицу длины соленоида,
число витков на единицу длины соленоида,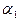 и
и 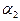 - углы, под которыми из точки А видны концы соленоида
- углы, под которыми из точки А видны концы соленоида 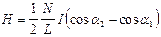 .
.
на оси в точке, удаленной от концов: 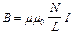 ,
, 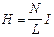
в точках оси, совпадающих с ее концами: 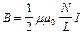 ,
, 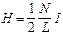 .
.
Для бесконечно длинного соленоида 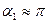
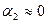 , т.е.
, т.е. 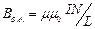
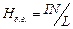
Магнитный момент соленоида равен геометрической сумме магнитных моментов всех его витков: 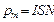 .
.
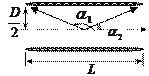
Задача 7. Каким должно быть отношение длины катушки к ее диаметру, чтобы магнитное поле в центре катушки можно было рассматривать как поле бесконечно длинного соленоида. Ошибка при таком допущении не должна превышать 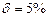 . Указание:
. Указание: 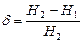 , где
, где 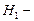 напряженность поля внутри катушки конечной длины и
напряженность поля внутри катушки конечной длины и 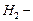 напряженность поля внутри бесконечно длинной катушки.
напряженность поля внутри бесконечно длинной катушки.
 2014-02-02
2014-02-02 20023
20023

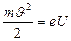 и
и 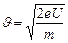 . Со стороны магнитного поля на электрон действует сила Лоренца. Направление силы Лоренца определяется по правилу
. Со стороны магнитного поля на электрон действует сила Лоренца. Направление силы Лоренца определяется по правилу  . Т.к.
. Т.к. 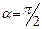 , то
, то 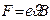
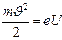 и
и 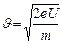 . Со стороны магнитного поля на электрон действует сила Лоренца, перпендикулярная вектору магнитной индукции и вектору скорости частицы:
. Со стороны магнитного поля на электрон действует сила Лоренца, перпендикулярная вектору магнитной индукции и вектору скорости частицы: 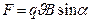 . Т.к.
. Т.к. 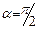 , то
, то 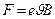 Т.к. начальная скорость электрона перпендикулярна индукции, то его траектория лежит в одной плоскости. Работа силы Лоренца равна нулю, значит
Т.к. начальная скорость электрона перпендикулярна индукции, то его траектория лежит в одной плоскости. Работа силы Лоренца равна нулю, значит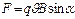 . Т.к. сила Лоренца всегда перпендикулярна к скорости, то величина скорости не будет изменяться под действием этой силы. Но при постоянной скорости величина силы тоже будет постоянной. Из механики известно, что постоянная сила, перпендикулярная к скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле, будет двигаться по окружности в плоскости, перпендикулярной полю, со скоростью, равной поперечной составляющей
. Т.к. сила Лоренца всегда перпендикулярна к скорости, то величина скорости не будет изменяться под действием этой силы. Но при постоянной скорости величина силы тоже будет постоянной. Из механики известно, что постоянная сила, перпендикулярная к скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле, будет двигаться по окружности в плоскости, перпендикулярной полю, со скоростью, равной поперечной составляющей 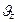 скорости; одновременно он
скорости; одновременно он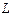 охватывает ток
охватывает ток 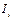 ) (
) (






