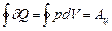Новосибирск

Ответы

Ответы

Задачи

Задачи

Задачи

Ответы

5.2. ;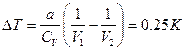

5.3. Газ охладится, , ;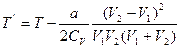

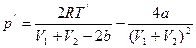5.5. , ;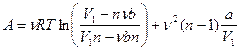

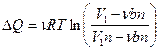5.6. ;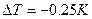

5.7. а) ,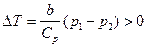

1.1. Найти уравнение политропы для идеального газа, теплоемкость C_v которого не зависит от температуры. Рассмотреть частные случаи: а) С= C_v, б) С= C_p, в) С=0, г) С=∞.

1.2. Выразить С политропического процесса через постоянные R, γ, n.

1.3 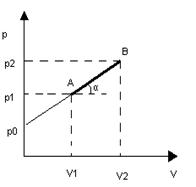. При каких значениях показателя политропы n идеальный газ при сжатии нагревается, а при каких охлаждается? Нагревается или охлаждается идеальный газ и какова его молярная теплоемкость, если он расширяется по закону:

а) pV²=const; б) p²V=const?

1.4. Найти уравнение процесса для идеального газа, при котором теплоемкость газа меняется с температурой по закону С= αТ, где α – постоянная.

Рис.3

11

Исследования Джоуля и Томсона позволили не только экспериментально подтвердить зависимость внутренней энергии реального газа от его объема. Было открыто важное физическое явление, получившее название эффекта Джоуля-Томсона.

Рис.4

Рис.19

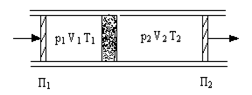В опыте использовалась теплоизолированная трубка, разделенная пористой перегородкой, по обе стороны от которой находился газ (рис.19). Газ под действием разности давлений медленно протекал через перегородку, при помощи поршней П₁, П₂ в этих условиях в каждый момент времени газ находился в термодинамически равновесных состояниях, давление p₁, p₂ по разные стороны перегородки поддерживалось постоянным.

Стационарное течение газа через пробку называется процессом Джоуля-Томсона, а изменение температуры газа при таком течении – эффектом Джоуля-Томсона.

Процесс Джоуля-Томсона необратимый, он происходит при постоянной энтальпии:

.

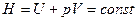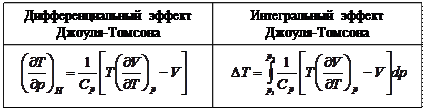
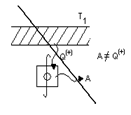
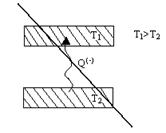
При достаточно низкой температуре газ при расширении охлаждается, 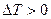- отрицательный эффект Джоуля-Томсона; при достаточно высокой температуре газ при расширении нагревается, 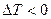- положительный эффект Джоуля-Томсона. Температура, при которой 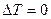, т.е. происходит изменение знака эффекта Джоуля-Томсона, называется температурой инверсии.

28

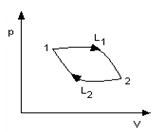
На диаграмме цикл изображается замкнутой кривой (рис.4). Проинтегрировав по циклу равенство, выражающее первое начало термодинамики, получим важный результат:

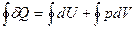
(5)

	Ац=Q(+)+Q(-)

(6)

Циклические процессы являются основой действия тепловых машин. Если цикл идет по часовой стрелке, то машина работает в режиме двигателя (рис.5), если против часовой стрелки, то в режиме холодильника или кондиционера (рис.6).

Рис.7

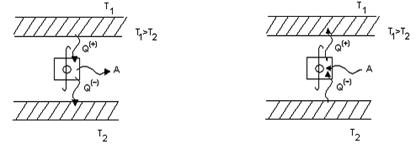
Рис.5. Схема работы двигателя Рис.6. Схема работы холодиль-

ной машины

Циклический процесс, единственным результатом которого было бы производство работы за счет уменьшения внутренней энергии теплового резервуара, невозможен. (Второе начало термодинамики, формулировка Кельвина.)

Эффективность двигателя характеризуется коэффициентом полезного действия 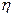(КПД).

Эффективность холодильника, кондиционера – коэффици-

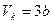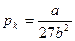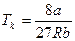, , . (24)

В критическом состоянии вещество обладает весьма интересными свойствами. В критической точке исчезает разница между жидкостью и газом, вещество становится физически однородным и продолжает оставаться таким при дальнейшем нагревании, при Т >Т_кр газ не может быть превращен в жидкость ни при каком давлении. При Т_кр поверхностное натяжение, теплота парообразования обращаются в нуль, сжимаемость вещества, наоборот, бесконечно велика. В критической точке давление (плотность) не зависит от объема, т.е. если в некоторой области плотность частиц увеличивается, то не возникает сил давления, которые стремились бы эту плотность уменьшить, и наоборот. Кроме того, в критической точке (критическом состоянии) теплоемкости С_p,C_V = ∞, установление равновесного состояния происходит очень медленно (десятки часов).

4.1. Записать уравнение Ван-дер-Ваальса (21) для газа, содержащего 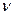молей.

4.2. Рассчитать критические параметры p_k, V_k, T_k двумя способами, учитывая, что для критического состояния уравнение (21) имеет вид (V-V_кр)³=0.

4.3. Записать уравнение Ван-дер-Ваальса в приведенных параметрах

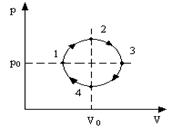2.1. Циклический процесс представлен в координатах (p,V) в форме окружности с центром в точке (p₀,V₀), максимальный объем и давление равны соответственно V_max и p_max (рис.8). Изобразить на графике работу расширения, сжатия. Найти:

а) работу расширения;

б) работу сжатия;

Рис.8

в) работу за цикл.

2.2. У тепловой машины, работающей по циклу Карно, температура нагревателя в α раз больше температуры холодильника. За один цикл машина производит работу А. Какая работа за цикл затрачивается на изотермическое сжатие? Решить эту же задачу, считая α=1,6; А=12 кДж.

2.3. В каком случае КПД цикла Карно повысится больше: при увеличении температуры нагревателя на ∆Т или при уменьшении температуры холодильника на такую же величину?

2.4. Найти КПД цикла, проводимого с идеальным газом и состоящего из двух изотерм с температурами Т₁ и Т₂ и двух изохор с объемами V₁ и V₂.(Т₁>T_2, V₁>V₂)

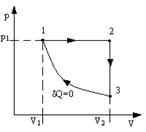2.5. На рис.9 изображена диаграмма обратимого цикла, выполняемого молем идеального газа в некоторой тепловой машине. Найти КПД цикла, выразив его как функцию температур Т₁, Т₂, Т₃. Процесс 3-1 адиабатический.

Рис.9

2.6. Идеальный газ совершает цикл, состоящий из чередующихся изотерм и адиабат (рис.10). Температуры, при которых происходят изотермические процессы, равны Т₁, Т₂, Т₃. Найти КПД такого цикла, если при каждом изотермическом расширении объем газа увеличивается в одно и тоже число раз.

Функция имеет минимум, в котором силы притяжения уравновешиваются силами отталкивания. Аналитический вид функции 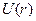на полуэмпирической основе представлен ниже:

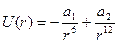- потенциал Леннарда-Джонса (20)

Рис.17

Рис.17

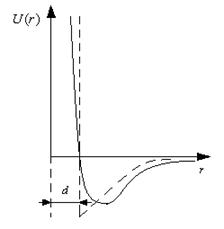
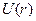Уравнений состояний для реальных газов множество, наиболее простое из них – уравнение Ван-дер-Ваальса. В теории Ван-дер-Ваальса используется упрощенная модель межмолекулярного взаимодействия, часть кривой заменяется вертикальной прямой (пунктирная линия на рис.17). Если d – расстояние до этой прямой от начала координат, то центры взаимодействия частиц не могут сблизиться на расстояние, меньшее d, что соответствует модели твердых упругих шаров, описываемой уравнением состояния газа Ван-дер-Ваальса.

2.10. В помещении необходимо поддерживать температуру 25˚С, когда температура наружного воздуха 35˚С. Обеспечит ли требуемую температуру кондиционер, который при работе по циклу Карно в качестве тепловой машины имеет η=5%; на основе теоремы Карно оценить КИЭ данной машины.

2.11. Сделайте оценку (сверху) КИЭ бытового холодильника, если температура морозильной камеры - 20˚С.

2.1.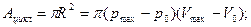

2.2.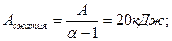

2.3. во втором;

2.4.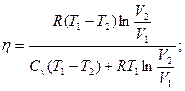

2.5.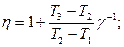

2.6.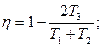

2.7.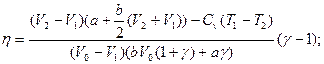

2.8.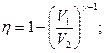

2.9.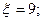

2.10. да;

2.11.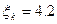

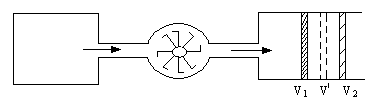находящийся при температуре Т₁=300˚К, расширяется без подвода и отдачи тепла в пустой сосуд через турбину, необратимым образом совершая работу (рис.16). После установления равновесия температура газа понижается до Т=200˚К.

Рис.16

После этого газ квазистатически сжимается: сначала изотермически, а затем адиабатически, возвращаясь в первоначальное состояние. При этом сжатии затрачивается работа А=15кДж. Найти изменение энтропии газа при расширении.

3.8. Вычислить изменение энтропии при смешении одноатомного идеального газа массы m₁, имеющего начальную температуру Т₁ и давление p₁, и двухатомного газа массы m₂, имеющего начальные температуру Т₂ и давление p₂. Молярные массы смешиваемых газов М₁ и М₂.

3.1.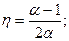

3.2.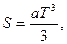

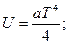
3.3.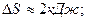

3.4.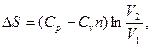

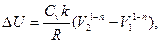
где k=const;

3.5.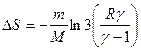

Рис.13

Рис.14

Самая краткая и исчерпывающая формулировка второго начала – энтропия есть функция состояния системы. Все остальные формулировки являются строго логически доказуемыми следствиями этой аксиомы. Именно в этом духе сформулировал второе начало термодинамики А.Зоммерфельд в развернутой двухчастной форме.

Часть первая. Каждая термодинамическая система обладает функцией состояния, называемой энтропией. Энтропия вычисляется следующим образом. Система переводится из произвольно выбранного начального состояния в соответствующее конечное состояние через последовательность состояний равновесия. Вычисляются все подводимые при этом к системе порции тепла 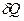, делятся каждая на соответствующую ей абсолютную температуру Т и все полученные таким образом значения суммируются.

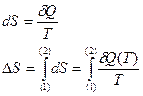(13)

Часть вторая. При реальных (не идеальных) процессах энтропия замкнутой системы возрастает.

Содержание второй части формулировки А.Зоммерфельда в большинстве учебников рассматривается как самодостаточная формулировка второго начала, или как закон возрастания