| Выполнению норм выработки, % (х) | Количество рабочих, человек (f) |
| 97.5 | |
| 102.5 | |
| 107.5 | |
| 112.5 | |
| 117.5 | |
| 122.5 | |
| ИТОГО |
1) Т.к. данные сгруппированы, т.е. известна частота (количество рабочих), то среднее значение нужно рассчитывать по формуле средней арифметической взвешенной: 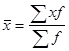 .
. Однако, для этого необходимо найти середины интервалов. Подобная процедура детально описана в задаче №5 темы «Средние величины». После такой процедуры исходные данные можно записать в виде следующего ряда распределения:
Однако, для этого необходимо найти середины интервалов. Подобная процедура детально описана в задаче №5 темы «Средние величины». После такой процедуры исходные данные можно записать в виде следующего ряда распределения:
Тогда среднее значение нормы выработки определиться следующим образом: 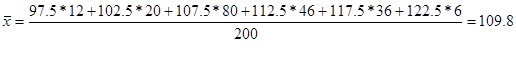
Для удобства расчета показателей вариации построим следующую таблицу:
| Выполнению норм выработки, % (х) | Количество рабочих, человек (f) | Отклонение от среднего значения (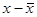 ) )
| 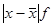
| 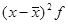
|
| 97.5 | -12,3 | 147,6 | 1815,48 | |
| 102.5 | -7,3 | 1065,8 | ||
| 107.5 | -2,3 | 423,2 | ||
| 112.5 | 2,7 | 124,2 | 335,34 | |
| 117.5 | 7,7 | 277,2 | 2134,44 | |
| 122.5 | 12,7 | 76,2 | 967,74 | |
| ИТОГО | - | 955,2 |
2) Размах вариации определяется по формуле: 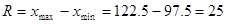
3) Среднее линейное отклонение: 
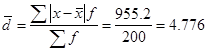
4) Дисперсия: 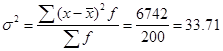
5) Среднее квадратическое отклонение: 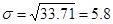
Далее рассчитаем относительные показатели вариации.
6) коэффициент осцилляции: 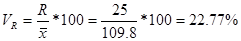
7) линейный коэффициент вариации: 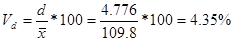
8) коэффициент вариации: 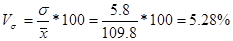 , т.к. значение меньше 33% можем сделать вывод о том, что данная совокупность однородна.
, т.к. значение меньше 33% можем сделать вывод о том, что данная совокупность однородна.
Задача № 2/ Оценить взаимосвязь между разрядом токаря и количеством изготовляемых деталей при помощи дисперсионного анализа при таких исходных данных:
| Токари 4 разряда | Токари 5 разряда | ||
| Фамилия рабочего | Количество деталей, шт | Фамилия рабочего | Количество деталей, штук |
| А | Ж | ||
| Б | З | ||
| В | И | ||
| Г | К | ||
| Д | Сумма | ||
| Е | |||
| Cумма |
 2014-02-24
2014-02-24 343
343







