Для вывода универсальной зависимости, связывающей параметры состояния в термодинамических процессах, воспользуемся следующими уравнениями (1.27, 1.28) первого закона термодинамики и с учетом выражений (1.1, 1.9, 1.29, 1.30) напишем их в виде:
c×dT=cv× dT + p×dv, (а) (1.31)
c× dT=cp× dT - v×dp. (б) (1.32)
Разделив уравнение (б) на уравнение (а), найдем
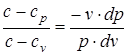 . (1.33)
. (1.33)
Введем обозначение 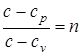 . После интегрирования (1.33) и ряда несложных алгебраических преобразований, получаем
. После интегрирования (1.33) и ряда несложных алгебраических преобразований, получаем
p·vn=const. (1.34)
Последнее уравнение является уравнением политропного процесса, где n - называется показателем политропы, который меняется в пределах -¥ < n < ¥. Политропным называется процесс, в котором происходит изменение всех термодинамических функций состояния, за исключением удельной теплоемкости, которая остается постоянной величиной в течение данного процесса.
Решая зависимость 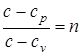 относительно с, находим выражение для удельной теплоемкости политропного процесса
относительно с, находим выражение для удельной теплоемкости политропного процесса
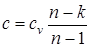 , (1.35)
, (1.35)
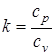 - показатель адиабаты.
- показатель адиабаты.
Из выражения (1.35) следует, что теплоемкость ТДС (рабочего тела) зависит от характера протекающего термодинамического процесса (на что указывает показатель политропы n) и от физических свойств рабочего тела через коэффициент показателя адиабаты k)
Рассматривая формулу (1.34) совместно с уравнением состояния p×v=Rг×T, можно представить ее еще в следующих эквивалентных формах:
T× vn-1= const; Tn× p1-n = const. (1.36)
 2014-02-24
2014-02-24 782
782








