Решение. Необходимо найти: p1, t2, V2, L

Дано: V₁, m_см, p₂, t₁, , , .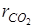

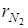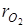Необходимо найти: p₁, t₂, V₂, L_1-2, Δ U=U₂–U₁.

1. Сначала схематично представим рассматриваемый процесс в pv - и Ts - диаграммах, следуя рис. 4.1.

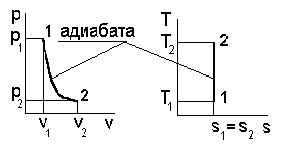
Рис. 4.1

2. Состояние исследуемой газовой смеси описывается уравнением Клапейрона - Менделеева (см. формулу 1), которое в обозначениях, принятых в данной задаче, можно представить в виде

p·V=m_см·R_см·T. (4.1)

Газовая смесь из состояния 1 переходит в состояние 2 по адиабате, поэтому параметры начального и конечного состояний смеси связаны с уравнениями (1.59, 1.60, 1.61). Применительно ко всему объему (V_i=m_см·v_i) эти уравнения принимают вид

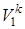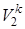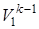p₁ ·= p₂ ·; T₁· = T₂· 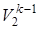; T₁^k ·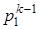= T₂^k ·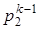. (4.2)

Из структуры формулы (4.1) следует, что, в начале необходимо определить газовую постоянную смеси R_см. Для этого используем формулу (1.18):

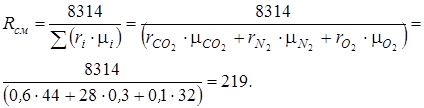
Анализ процесса сжатия смеси осуществляется при помощи уравнений (4.2), но прежде необходимо найти показатель адиабаты 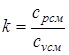, для нахождения значения которого нужно рассчитать изобарную c_pсм и изохорную c_vсм теплоемкости смеси, используя формулы (1.22,1.21):

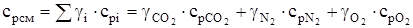
. (4.3)

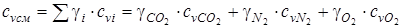
По условию рассматриваемой задачи смесь задана объемными долями r_i, а в формулах (4.3) состав смеси выражен в массовых долях γ_i. Перевод в массовые доли производим при помощи формулы (1.19):

.

.

.

.

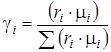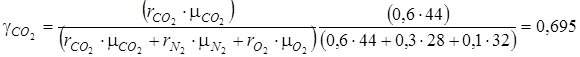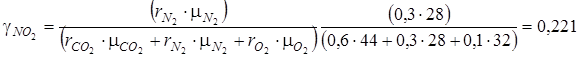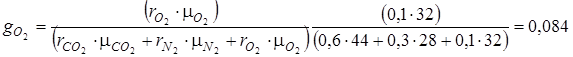Из [П.1] находим значения мольных изобарных и изохорных теплоемкостей компонентов газовой смеси

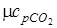= 37,4; 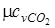= 29,1

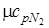= 29,1; 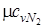= 20,8

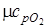= 29,1; 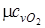= 20,8

Переводим значения мольных теплоемкостей в массовые с помощью формул:

;

;

;

;

;

;

.

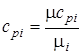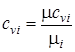
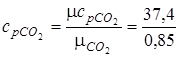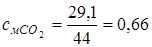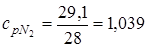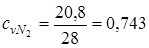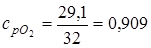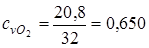Найденные массовые доли компонентов газовой смеси γ_i и их изобарные, изохорные теплоемкости подставляем в уравнения (4.3):

c_pсм =0,695·0,85+0,221·1,039+0,084·0,909=0,8967.

c_vсм =0,695·0,66+0,221·1,743+0,084·0,650=0,6775.

Определяем значение показателя адиабаты:

.

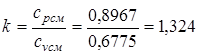Формулу (4.1) напишем применительно к начальному состоянию смеси

р₁V₁=m_см ·R _см ·T₁,

где T₁=t₁ +273.

Из последнего выражения находим начальное давление:

.

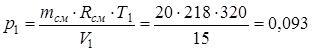Далее в соответствии с первой из формул (4.2) p₁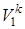=p₂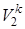 определяем конечный объем смеси:

.

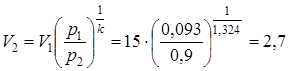Пользуясь второй из формул (4.2) T₁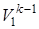=T₂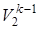, рассчитываем конечную температуру смеси:

.

.

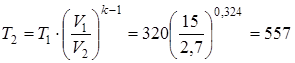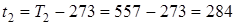Обращаясь к формуле (1.63), находим удельную работу сжатия газовой смеси:

.

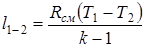Применительно ко всей массе смеси работа сжатия равна

.

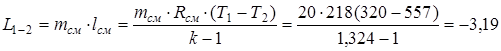Отрицательное значение L_1-2 означает, что эта работа внешних сил над газовой смесью.

Изменение удельной внутренней энергии смеси определяем, используя формулу (1.64)

Δ u =(u₂-u₁)= c_v·(T₂-T₁).

Применительно ко всей массе смеси изменение внутренней энергии равно

Δ U = U₂-U₁=m_см ·(u₂-u₁)=m_см ·c_v·(T₂-T₁)=

= 20·0,6775(557-320)=3,19.

Определяем парциальные давления компонентов газовой смеси. Из закона Бойля - Мариотта следует

.

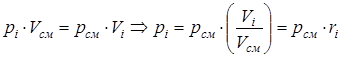Используя последнее выражение, определяем парциальные давления компонентов газовой смеси:

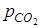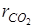=· p₂ =0,6·0,9=0,54,

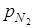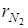=· p₂ =0,3·0,9=0,27,

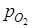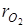=· p₂ =0,1·0,9=0,09.

Пример 2. Рассчитать цикл ДВС с изохорным подводом теплоты (цикл Отто), если начальные параметры рабочего тела p₁ =0,1 МПа, t₁ =20 ˚C, степень сжатия ε=6,5, а отведенная теплота | q₂ |=320 кДж/кг. Определить параметры состояния рабочего тела в характерных точках цикла, подведенное количество теплоты q₁, работу цикла l_ц и термический КПД η _t, а также термический КПД цикла Карно в том же диапазоне температур. Изобразить цикл в координатах p, v и T, s. Рабочее тело - воздух. Средняя изохорная теплоемкость
c_vm =0,716 кДж/(кг·К); удельная газовая постоянная R_в =287 Дж/(кг·К); показатель адиабаты k =1,4.