Раздел 3. Квантование сигналов
Тема 6. Квантование сигналов. Способы разбиения шкалы сигнала на отдельные уровни. Способы отождествления текущего значения сигнала с уровнем квантования. Шумы квантования.
Квантование сигналов, как отмечалось выше, заключается в замене текущего значения непрерывного сигнала U (t) или U (kT Д) одним из конечного числа N уровней квантования. Обозначим номера уровней квантования как 0, 1, 2, …, N -1.
Наиболее часто применяют равномерное квантование, при котором расстояние Δ U между двумя соседними уровнями, называемое шагом квантования, одинаковое для всего диапазона изменения непрерывного сигнала.
Шкала U значений сигнала в произвольный момент времени ti, который при дискретизации сигналов совпадает с моментами взятия дискретных отсчетов kТ Д, может быть разбита на отдельные уровни квантования различными способами (рисунок 6.1).
Для случая, показанного на рисунке 6.1,а, начальный уровень квантования, то есть уровень с номером 0, совмещается с началом U мин шкалы сигнала, а последний, то есть уровень с номером N –1, – с концом U макс шкалы. При этом шаг квантования определяется выражением
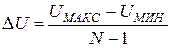 . (6.1)
. (6.1)
Для случая на рисунке 6.1,б начальный уровень квантования находится выше начала U мин шкалы сигнала на 0.5Δ U, а последний уровень – на 0.5Δ U
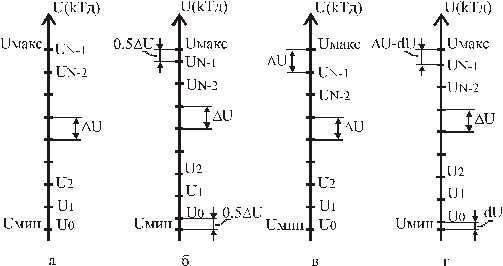
Рисунок 6.1 – Способы разбиения шкалы сигнала на отдельные уровни
ниже конца U макс шкалы. Шаг квантования в этом случае определяется как
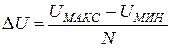 . (6.2)
. (6.2)
В случае, представленном на рисунке 6.1,в, начальный уровень квантования совмещается с началом шкалы сигнала, а последний уровень отстоит от конца шкалы на один шаг квантования Δ U. Шаг квантования при этом определяется выражением (6.2).
В описанных выше вариантах положение начального уровня, а, следовательно, и конечного, является фиксированным. В некоторых типах аналого-цифровых преобразователей начальный уровень принципиально не может быть привязан к началу шкалы сигнала. Примером такого АЦП является АЦП последовательного счета и построенные на его основе интегрирующие АЦП. В этих АЦП амплитуда отсчета сигнала U (kT д) преобразуется в пропорциональный временной интервал, который заполняется импульсами с большой частотой повторения. В этом случае реализуется вариант разбиения шкалы сигнала на уровни, показанный на рисунке 6.1,г. Нулевой уровень смещен относительно начала шкалы на некоторую случайную величину dU, 0≤ dU <Δ U. При этом последний уровень смещен относительно конца шкалы также на случайную величину Δ U – dU. Шаг квантования в данном случае также определяется выражением (6.2).
Для отождествления текущего значения отсчета U (kT д) с соответствующим уровнем квантования применяют два способа:
– сигнал U (kT д) отождествляют с ближайшим уровнем квантования;
– сигнал U (kT д) отождествляют с ближайшим меньшим уровнем квантования.
Квантование по уровню неизбежно приводит к погрешности представления сигнала. Эту погрешность называют погрешностью квантования или шумом квантования. Максимальная погрешность квантования Δкв зависит от способа отождествления сигнала с соответствующим уровнем квантования. В первом случае она, очевидно, равна половине шага квантования, Δкв1=0.5Δ U, а во втором случае – шагу квантования, Δкв2=Δ U.
Квантуемый сигнал является случайной величиной. При большом числе уровней квантования, что обычно выполняется на практике, закон распределения этой случайной величины внутри каждого шага квантования равномерный, то есть плотность распределения внутри каждого шага квантования постоянна. Исходя из этого, можно определить среднеквадратическую погрешность σкв квантования сигнала. Для первого способа отождествления сигнала с уровнем квантования
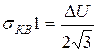 . (6.3)
. (6.3)
Для второго способа погрешность квантования
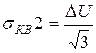 . (6.4)
. (6.4)
Итак, мы заменили текущее значение каждого отсчета соответствующим уровнем квантования (рисунок 6.2, верхний график). Каждый уровень квантования характеризуется его номером, представленном в двоичном коде. Число разрядов двоичного кода n связано с максимальным числом уровней N соотношением
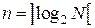 , (6.5)
, (6.5)
где знак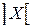 означает округление до ближайшего большего целого числа.
означает округление до ближайшего большего целого числа.
Если сигналы разрядов передаются одновременно по разным линиям, то это код называют параллельным (рисунок 6.2,1)).
Если сигналы разрядов передаются по одной и той же линии один за другим, то получим последовательный код (рисунок 6.2,2)).
 2014-02-24
2014-02-24 2568
2568








