Постановка задачи
Постановка конкретной задачи принятия решений (ЗПР) включает:
- формулировку задачи;
- определение типа задачи;
- выбор метода решения;
- определение множества альтернатив и основных критериев для выбора из них наилучшей и согласование критериев.
Для решения задач широко применяются различные методы.
При построении, изучении и применении экономико-математических моделей принятия решений используются различные математические методы, именуемые экономико-математическими. Их можно разделить на несколько групп:
- методы оптимизации;
- методы, учитывающие неопределенность, прежде всего вероятностно-статистические;
- методы построения и анализа имитационных моделей;
- методы анализа конфликтных ситуаций (теории игр).
Во всех этих группах можно выделить статическую и динамическую постановки. При наличии фактора времени используют дифференциальные уравнения и разностные методы.
Математическое программирование – это семейство инструментальных средств, созданных для помощи в процессе решения управленческих задач, при котором лицо, принимающее решения, должно выделить ограниченные ресурсы для различных действий или операций с условием оптимизации измеримой цели. Наиболее известным методом этого семейства инструментов является линейное программирование. Оно широко используется в информационных системах поддержки руководителя (ИСПР) и имеет много важных практических приложений, например решение задачи распределения (ресурсов или времени).
Задачи распределения, решаемые на основе линейного программирования, обычно отражают следующие характеристики:
- для распределения доступно ограниченное количество ресурсов;
- ресурсы используются в производстве продукции или услуг;
- существует два или более путей использования ресурсов, каждый из которых называется решением или программой;
- распределение обычно ограничивается несколькими доступными пределами и требованиями, называемыми ограничениями.
Модель распределения линейного программирования основывается на следующих различных экономических допущениях:
- отдача или доходность при различных вариантах распределения могут сравниваться, т.е. они могут быть измерены в общих единицах
(например, денежных);
- отдача от одного распределения независима от других распределений;
- общая доходность является суммой доходностей, принесенных различными действиями;
- все исходные данные известны и определены.
Наиболее известны задачи линейного программирования, в которых максимизируемая функция F(X) является линейной, а ограничения А задаются линейными неравенствами.
Пример [4]. Цех может производить стулья и столы. На производство стула идет 5 единиц материала, на производство стола – 20 (футов красного дерева). Трудоемкость изготовления одного стула 10 человеко-часов, стола – 15. Имеется 400 единиц материала и 450 человеко-часов. Прибыль при производстве стула – 45 долларов США, при производстве стола −
80 долларов США. Сколько надо сделать стульев и столов, чтобы получить максимальную прибыль?
Введем обозначения: Х1 – число изготовленных стульев;
Х2 – число сделанных столов. Задача оптимизации имеет вид:
45 Х1 + 80 Х2 → max;
5 Х1 + 20 Х2 ≤ 400;
10 Х1 + 15 Х2 ≤ 450;
Х1 ≥ 0;
Х2 ≥ 0.
В первой строке выписана целевая функция − прибыль при выпуске Х1 стульев и Х2 столов. Ее требуется максимизировать, выбирая оптимальные значения переменных Х1 и Х2. При этом должны быть выполнены ограничения по материалу (вторая строчка) − может быть истрачено не более 400 футов красного дерева, а также и ограничения по труду (третья строчка) − работы выполнялись в течение 450 часов. Кроме того, нельзя забывать, что числа столов и стульев положительны.
В четвертой и пятой строчках задачи и констатируется, что переменные неотрицательны.
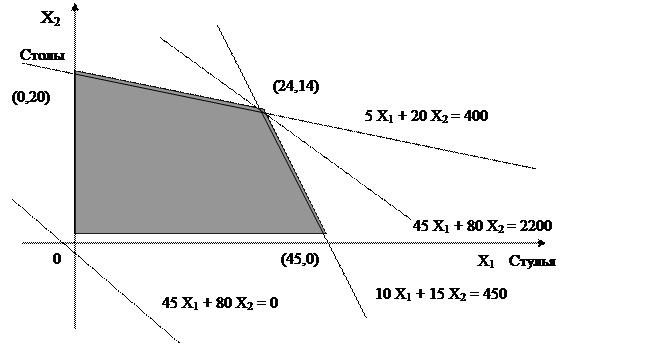
Условия производственной задачи можно изобразить на координатной плоскости. По горизонтальной оси абсцисс будем откладывать значения Х1, а по вертикальной оси ординат − значения Х2.
 | |||
|
Таким образом, множество возможных значений объемов выпуска стульев и столов (Х1, Х2) представляет собой выпуклый четырехугольник, показанный на рисунке 4. Три его вершины очевидны − это (0,0), (45,0) и (0,20). Четвертая − это пересечение двух прямых, т. е. решение системы уравнений следующее:
 5Х1 + 20Х2 = 400;
5Х1 + 20Х2 = 400;
10Х1 + 15Х2 = 450.
Из первого уравнения: 5Х1 = 400 − 20Х2; Х1 = 80 − 4Х2. Подставляем во второе уравнение: 10(80 − 4Х2) + 15Х2 = 800 − 40Х2 + 15Х2 =
= 800 − 25Х2 = 450, следовательно, 25Х2 = 350, Х2 = 14. Отсюда
Х1 = 80 − 4×14 = 80 − 56 = 24. Итак, четвертая вершина четырехугольника − это (24, 14).
Основная идея линейного программирования состоит в том, что максимум достигается в вершинах многоугольника. Максимум целевой функции, равный 2200, достигается в вершине (24, 14).
Таким образом, оптимальный выпуск таков: 24 стула и 14 столов. При этом используется весь материал и все трудовые ресурсы, а прибыль равна 2200 долларам США.
 2014-02-24
2014-02-24 3228
3228
