1) Случай функции двух переменных 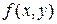 . Направление задается вектором. Выберем единичный вектор, задающий направление на плоскости:
. Направление задается вектором. Выберем единичный вектор, задающий направление на плоскости: 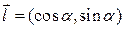 . Этот вектор образует угол
. Этот вектор образует угол 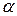 с положительным направлением оси OX. Производной функции двух переменных по направлению
с положительным направлением оси OX. Производной функции двух переменных по направлению 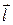 называется выражение
называется выражение 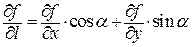 .
.
2) Случай функции трех переменных 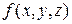 . Пусть задан единичный вектор
. Пусть задан единичный вектор 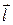 , образующий углы
, образующий углы 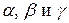 с осями OX, OY и OZ, соответственно. Если обозначить координаты вектора
с осями OX, OY и OZ, соответственно. Если обозначить координаты вектора 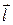 через
через 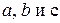 , то по формуле косинуса угла между двумя векторами
, то по формуле косинуса угла между двумя векторами 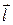 и
и 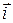 получим
получим 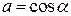 . Аналогично,
. Аналогично, 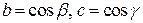 . Таким образом, единичный вектор, образующий углы
. Таким образом, единичный вектор, образующий углы 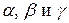 с осями OX, OY и OZ, имеет координаты
с осями OX, OY и OZ, имеет координаты 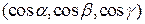 . Производной функции трех переменных по направлению
. Производной функции трех переменных по направлению 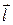 называется выражение
называется выражение
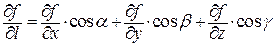 .
.
Определение. Градиентом функции 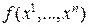 называется вектор
называется вектор 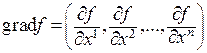 . Поэтому производную функции по направлению, задаваемому единичным вектором
. Поэтому производную функции по направлению, задаваемому единичным вектором 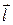 , можно вычислить по формуле
, можно вычислить по формуле 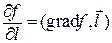 , где справа в формуле стоит скалярное произведение градиента функции и единичного вектора направления.
, где справа в формуле стоит скалярное произведение градиента функции и единичного вектора направления.
Основное свойство градиента: среди всевозможных направлений наибольшее, причем положительное, значение производная по направлению принимает по направлению градиента. Это свойство следует из определения скалярного произведения. Поскольку положительность производной означает рост функции, направление градиента в точке – это направление наибольшего роста функции.
Частные производные высших порядков.
Любая частная производная 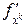 функции
функции 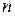 переменных
переменных 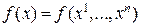 сама также является функцией
сама также является функцией 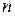 переменных. Частная производная от частной производной функции многих переменных называется частной производной второго порядка функции
переменных. Частная производная от частной производной функции многих переменных называется частной производной второго порядка функции 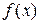 . При этом, если переменные, по которым берутся производные сначала от функции
. При этом, если переменные, по которым берутся производные сначала от функции 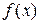 , а затем от функции
, а затем от функции 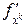 , не совпадают, такая частная производная называется смешанной. Обозначения частной производной второго порядка:
, не совпадают, такая частная производная называется смешанной. Обозначения частной производной второго порядка: 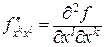 . В том случае, когда
. В том случае, когда 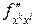 и
и 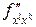 – непрерывные функции в окрестности некоторой точки,
– непрерывные функции в окрестности некоторой точки, 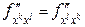 в этой точке.
в этой точке.
Аналогично вводятся частные производные любого порядка.
П р и м е р. Найти 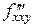 от функции
от функции 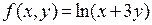 . Имеем
. Имеем 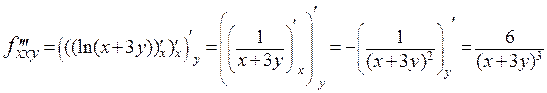 .
.
Для того, чтобы вычислить ту же производную с помощью MAXIMы, воспользуемся командой diff(log(x+3*y),x,2,y,1).
Дифференциалы высших порядков.
По аналогии с производными вводятся дифференциалы высших порядков, то есть дифференциалы от дифференциалов. Рассмотрим функцию трех переменных 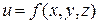 . Дифференциалом этой функции является выражение
. Дифференциалом этой функции является выражение 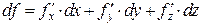 . Заметим, что входящие в последнее выражение производные – функции от
. Заметим, что входящие в последнее выражение производные – функции от 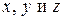 , а дифференциалы переменных не зависят от
, а дифференциалы переменных не зависят от 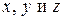 . Поэтому при условии непрерывности смешанных производных дифференциал второго порядка имеет вид
. Поэтому при условии непрерывности смешанных производных дифференциал второго порядка имеет вид
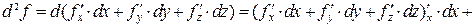
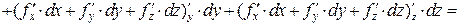
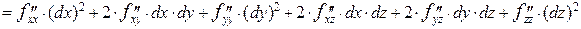 .
.
В последней формуле мы воспользовались свойством равенства смешенных производных. Нетрудно видеть, что формула дифференциала второго порядка аналогична формуле второй степени суммы трех слагаемых. Нетрудно сосчитать дифференциалы второго и третьего порядков функции двух переменных 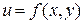 :
: 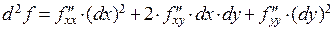 ,
,
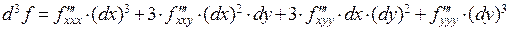 .
.
Упражнение. Найти 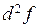 для функции
для функции 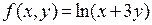 в точке (1,1).
в точке (1,1).
Формула Тейлора для функции многих переменных.
Как и в случае функций одной переменной, для функций многих переменных 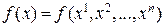 формула Тейлора дает связь между приращением функции в точке и ее дифференциалами в этой же точке:
формула Тейлора дает связь между приращением функции в точке и ее дифференциалами в этой же точке:
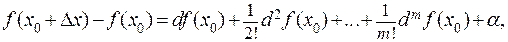
где 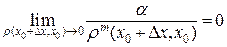 .
.
В частности, для функции двух переменных имеем:
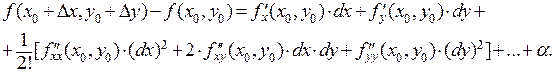
Здесь 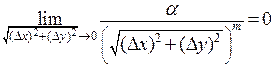 .
.
 2014-02-24
2014-02-24 3969
3969