Классификация событий
Определение. Случайным событием называется любой факт, который в результате испытания может произойти или не произойти.
Например: 1) появление герба при бросании монеты,
2) выигрыш автомобиля по билету лотереи,
3) выход бракованного изделия с конвейера завода.
Обозначают события заглавными буквами латинского алфавита: A, B, C, ….
Определение. Событие называется достоверным, если в результате испытания оно обязательно должно произойти.
Например, извлечение белого шара из ящика, в котором все шары белые.
Определение. Событие называется невозможным, если в результате оно вообще не может произойти.
Например, извлечение черного шара из ящика, в котором все шары белые.
Определение. Два случайных события  и
и 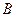 называются несовместными, если появление одного из них исключает появление другого в данном испытании.
называются несовместными, если появление одного из них исключает появление другого в данном испытании.
Например, выпадение орла и выпадение решки при однократном бросании монеты.
Определение. События  и
и 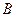 называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.
называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.
|
|
|
Например, получение студентом на зкзамене по одной дисциплине оценок отлично, хорошо, удовлетворительно – события несовместные, а получение тех же оценок на экзамене по трём дисциплинам – события совместные.
Определение. События называются равновозможными, если в результате испытания ни одно из этих событий не является объективно более возможным.
Например, извлечение туза или короля из колоды карт; появление герба или решки при бросании монеты.
Определение. Несколько событий образуют полную группу, если они попарно несовместны и в результате испытания появится только одно из этих событий.
Частным случаем событий, образующих полную группу, являются противоположные события.
Определение. Два несовместных события, из которых в результате испытания одно должно обязательно произойти, называются противоположными.
Обозначают противоположные события и
и 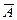 .
.
Например, при выстреле из ружья попадание – событие и промах - событие
и промах - событие 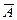 ; при бросании монеты выпадение орла – событие
; при бросании монеты выпадение орла – событие и выпадение решки – событие
и выпадение решки – событие 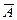 .
.
Для количественной оценки возможности появления случайного события вводится понятие вероятности. Существует два подхода к определению вероятности в зависимости от возможности проведения опыта. Если оценка осуществляется без опыта, то вероятность называется классической и обозначается 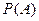 . Если есть возможность провести опыт, то вероятность называется статистической и обозначается
. Если есть возможность провести опыт, то вероятность называется статистической и обозначается 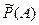 .
.
Определение. Вероятность события  равна отношению числа случаев благоприятствующих ему к общему числу всех равновозможных несовместных элементарных случаев, образующих полную группу
равна отношению числа случаев благоприятствующих ему к общему числу всех равновозможных несовместных элементарных случаев, образующих полную группу
|
|
|
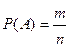 ,
,
где 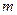 - число случаев благоприятствующих событию
- число случаев благоприятствующих событию  ;
;  – общее число всех возможных элементарных случаев.
– общее число всех возможных элементарных случаев.
Пример 1.1. Бросается игральная кость. Какова вероятность появления чётного числа очков?
Решение. Обозначим через событие  = {появление чётного числа очков}. Общее число исходов
= {появление чётного числа очков}. Общее число исходов 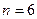
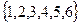 . Число случаев благоприятствующих событию
. Число случаев благоприятствующих событию 
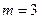
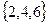 . Тогда вероятность появления четного числа очков равна
. Тогда вероятность появления четного числа очков равна 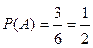 .
.
 2014-02-09
2014-02-09 812
812








