Для вычисления вероятности события необходимо уметь рассчитывать число различных комбинаций, т.е. уметь определять значения 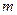 и
и  .
.
Определение. Размещением из  различных элементов по
различных элементов по 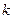 элементов называется соединение, которое отличается либо составом, либо порядком своих элементов.
элементов называется соединение, которое отличается либо составом, либо порядком своих элементов.
Число размещений обозначается символом 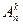 и вычисляется по формуле
и вычисляется по формуле
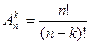 ,
,
где 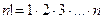 , причем 1! = 1, 0! = 1.
, причем 1! = 1, 0! = 1.
Пример 1.2. Сколько трехзначных чисел с неповторяющимися цифрами можно составить из цифр 1,2,3…9?.
Решение. Каждое трехзначное число является размещением из девяти цифр по три. Их число равно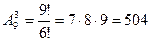 .
.
Определение. Сочетаниями из  элементов по
элементов по 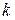 элементов называются соединения, которые различаются только составом своих элементов.
элементов называются соединения, которые различаются только составом своих элементов.
Число сочетанийобозначается символом 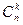 и вычисляется по формуле
и вычисляется по формуле
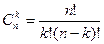 .
.
Пример 1.3. Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?
Решение. Т.к. порядок выбора деталей неважен, то взять 2 детали из имеющихся десяти можно 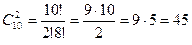 способами.
способами.
Определение. Перестановками из  элементов называются всевозможные соединения из этих
элементов называются всевозможные соединения из этих  элементов.
элементов.
Число перестановок обозначается символом 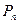 и вычисляется по формуле
и вычисляется по формуле
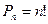 .
.
Пример 1.4. В конкурсе выступают 7 участников. Порядок их выступления определяется жребием. Сколько различных вариантов жеребьёвки при этом возможно? Решение. Каждый вариант жеребьёвки отличается только порядком участников конкурса, т.е. является перестановкой 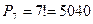 .
.
 2014-02-09
2014-02-09 4911
4911








