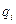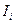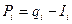2014-02-09
954
Актуарный метод
1. Рассчитан на срок больше года.
2. Начисление % происходит на уменьшающуюся часть основного долга по формуле:
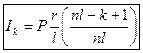(2.9.3)
3. Основной долг выплачивается равными частями, и эти части равны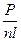 
.
4. Разовые погасительные платежи могут быть не равными по величине и образуют убывающий ряд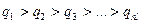 
. Но чаще всего погасительные платежи равны для удобства заемщика и их величину можно найти по формуле: 
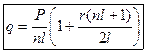(2.9.4)
Проценты по кредиту можно найти по формуле: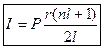 
(2.9.5) – сумма всех процентов (переплата).
5. При досрочном погашении кредита заемщик имеет возможность недоплатить банку определенное количество процентов по кредиту.
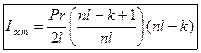(2.9.6) – формула остаточных процентов.
“Метод торговца” или “Правило 78”.
Рассчитан для сроков до 1,5 лет (краткосрочный).
Проценты начисляются на основную часть долга, которая не уменьшается с течением времени:
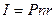
Разовые погасительные платежи одинаковы по величине:
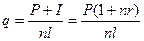
При погашении кредита досрочно заемщик имеет возможность не выплачивать определенную часть процентов по кредиту.
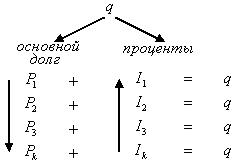
Пример:
Дано:
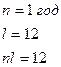
| Решение:
|
|
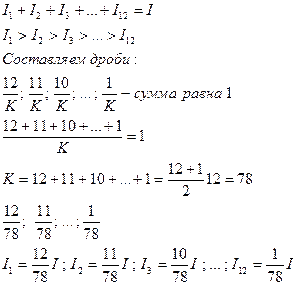
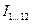
Пример:
Дано:
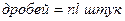
| Решение: общий случай
|
|
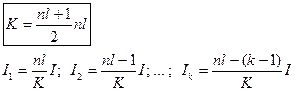
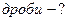
Пример:
Студент хочет купить ноутбук в кредит стоимостью 20 т.р. Кредит на полгода с ежемесячным погашением. Назначаемая ставка по кредиту 12 %. Составьте план погашения кредита.
Дано:
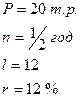
| Решение: частный случай
| ||||||||||||||||||||||||||||||||
|
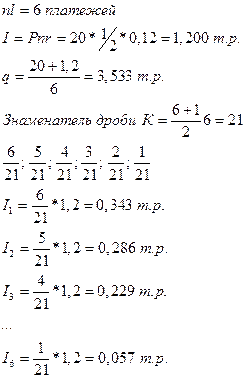
При досрочном погашении после 4 месяца заемщик имеет возможность не выплатить банку величину процентов равную 114 + 57 = 171 р.
В общем случае рассчитать остаточную часть процентов по кредиту можно по следующей формуле: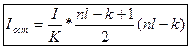 
(2.9.7) – формула остатка процентов при погашении кредита на k – том шаге.
